Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Производная функции комплексного переменного. Условия Коши — Римана

Понятие производной вводится для однозначной в D функции

w= {z).

О: Приращением функции w = 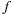(z) в т. z называется

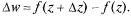
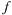Производной (z) функции w = (z) в т. z называется если предел существует и конечен при любом способе стремления к 0. Функция, имеющая производную в т. z, называется дифференцируемой в этой точке.

Для дифференцирования многозначной функции необходимо выделить ее однозначную ветвь.

Как и для функции действительного переменного, дифференцируемая в т. z функция (z) является непрерывной в т. z. Сохраняются основные правила дифференцирования, что следует из определения производной, правил алгебраических действий и справедливости теорем о пределах.

Т: Пусть u(х, у), v(x, у) дифференцируемы в т. z. Для того чтобы однозначная функция w = (z) = u(х, у) + iv(x, у) была дифференцируема в т. z = х + iy, необходимо и достаточно выполнения условий Коши—Римана:

(14.2)

Доказательство теоремы приведено в [18. С. 99]. Используя условия Коши—Римана (14.2), для (z) имеем следующие формулы:

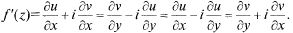(14.3)

Однозначные основные элементарные ФКП и однозначные ветви многозначных ФКП дифференцируемы в своих областях определения. Производные (z) вычисляются по тем же формулам, что и функции действительного переменного.

34. Условия Коши — Римана, называемые также условиями Даламбера — Эйлера — соотношения, связывающие вещественную и мнимую части всякой дифференцируемой функции комплексного переменного .