
Читайте также:
|
выражается следующей теоремой.
Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

36. Аналити́ческая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.
Однозначная функция  называется аналитической в точке
называется аналитической в точке 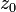 , если сужение функции
, если сужение функции  на некоторую окрестность
на некоторую окрестность 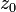 является аналитической функцией. Если функция аналитична в точке
является аналитической функцией. Если функция аналитична в точке 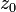 , то она аналитическая в каждой точке некоторой окрестности точки
, то она аналитическая в каждой точке некоторой окрестности точки 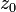 .
.
Аналитическая функция (комплексного переменного) — функция комплексного переменного 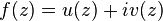 (где
(где 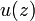 и
и  — вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в каждой точке некоторой области
— вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в каждой точке некоторой области  , называемой областью аналитичности, выполняется одно из трёх равносильных условий:
, называемой областью аналитичности, выполняется одно из трёх равносильных условий:
1. Для вещественной и мнимой части этой функции в каждой точке  выполняются условия Коши — Римана (аналитичность в смысле Коши — Римана);
выполняются условия Коши — Римана (аналитичность в смысле Коши — Римана);
2. Ряд Тейлора функции в каждой точке  сходится и его сумма равна
сходится и его сумма равна  (аналитичность в смысле Вейерштрасса);
(аналитичность в смысле Вейерштрасса);
3. Интеграл  для любой замкнутой кривой
для любой замкнутой кривой  (аналитичность в смысле Коши)
(аналитичность в смысле Коши)
В курсе комплексного анализа доказывается эквивалентность трёх определений.
Дата добавления: 2015-01-30; просмотров: 95 | Поможем написать вашу работу | Нарушение авторских прав |