Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

V Указания к пункту 4.

Получение оценок параметров

· Метод максимального правдоподобия

Суть метода - в качестве «наиболее правдоподобного» значения параметра берут значения, максимизирующее вероятность при опытах получить при опытах данную выборку (x₁, x₂,….,x_n)

Функцией правдоподобия непрерывной случайной величины называют функцию

Функцией правдоподобия дискретной случайной величины называют функцию

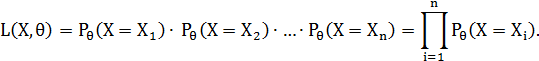
Оценкой максимального правдоподобия неизвестного параметра называют значение, при котором функция правдоподобия достигает максимума как функция от при фиксированных (x₁, x₂,…, x_n). Это значение параметра зависит от выборки и является искомой оценкой.

Функции L и lnL достигают максимума при одном и том же значении , поэтому для нахождения максимума функции правдоподобия L, можно искать max lnL и решать уравнение правдоподобия:

· Метод моментов

Начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. Теоретические моменты случайной величины зависят от параметра, а выборочные от элементов выборки. Выборочные моменты приближенно равны теоретическим. Приравняем их и получим уравнение, связывающее параметр и элементы выборки. Выразив параметр, получим функцию, которая и называется оценкой метода моментов. Для оценивания одного параметра обычно приравнивают выборочное среднее и математическое ожидание, для оценивания двух параметров используют еще выборочную и теоретическую дисперсию или начальные моменты второго порядка.

Для одного параметра: ; ;

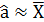
Для двух параметров: ;

Исследование свойств полученных оценок

· Несмещенность

Оценка 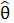параметра называется несмещенной, если =

Оценка 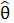параметра называется асимптотически несмещенной, если =

· Состоятельность

Оценка 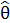параметра называется состоятельной, если т.е.

P(| при n ∞

Справедлива теорема: если

, D , то 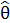– состоятельная оценка параметра

· Эффективность

Несмещенная оценка параметра называется эффективной, если её дисперсия равна нижней границе Рао-Крамера:

· Оптимальность

Для параметра может быть предложено несколько несмещенных оценок. Мерой точности несмещенной оценки считают её дисперсию D . Несмещенная оценка параметра называется оптимальной, если она имеет минимальную дисперсию среди всех несмещенных оценок этого параметра. Таким образом, эффективная оценка 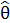является оптимальной.

· Нормальность

Исследуется точное или асимптотическое распределение оценки.

Можно использовать центральную предельную теорему:

Если случайные величины независимы, одинаково распределены и имеют конечные математические ожидания и дисперсии , , то при n→∞

, где

5. Задание: интервальное оценивание параметров.

Построение доверительных интервалов для каждого из параметров уровней значимости 0,05 и 0,01.