
Читайте также:
|
Верно ли что всякий линейный ограниченный оператор, действующий в банаховом простаранстве имеет ограниченный обратный
Нет. Теорема Банаха: Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство Е на банахово пространство Е1. Тогда обратный оператор  ограничен.
ограничен.
Банаховым пространством (B-пространством) называется нормированное линейное пространство, полное по метрике, порождённой нормой. Линейный оператор называется ограниченным снизу, если 
Теорема(Банах):Пусть  - биективный линейный ограниченный оператор из - биективный линейный ограниченный оператор из  в в  (оба Банаховы). Тогда (оба Банаховы). Тогда 
|
Верно ли что всякий линейный ограниченный оператор, действующий в банаховом простаранстве имеет ограниченный спектр
Да. Линейный ограниченный оператор имеет спектральный радиус, внутри шара с этим радиусом находится спектр
Верно ли, что линейный вполне непрерывный оператор, действующий в бесконечномерном банаховом простаранстве, не может иметь ограниченный обратный оператор
Нет. В бесконечномерном банаховом пространстве X компактный оператор A:X→ X не может иметь ограниченного обратного.
37. Определение функции распределения случайной величины. Пусть задано вероятностное пространство 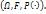 1.Случайной величиной называется вещественная ф-ия
1.Случайной величиной называется вещественная ф-ия  (отображение
(отображение  ), такая, что для любого вещественного
), такая, что для любого вещественного  множество
множество  , т.е. событие. 2.Вероятность
, т.е. событие. 2.Вероятность  называется ф-ей распределения случайной величины
называется ф-ей распределения случайной величины  . Свойства ф-ии распределения 1.Для
. Свойства ф-ии распределения 1.Для  2.
2.  3.
3.  непрерывна слева,
непрерывна слева,  . Пусть
. Пусть  Доказательство следует из того, что
Доказательство следует из того, что 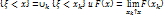 в силу непрерывности вероятности для монотонных последовательностей событий. 4.
в силу непрерывности вероятности для монотонных последовательностей событий. 4. 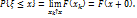 В этом случае для
В этом случае для  имеем
имеем 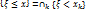 и далее используем непрерывность вероятности для монотонных последовательностей событий. 5.Выпишем соотношения для
и далее используем непрерывность вероятности для монотонных последовательностей событий. 5.Выпишем соотношения для  в частности, при
в частности, при  =F(
=F( 6.
6.  . Существование пределов следует из монотонности и ограниченности. Равенства из соотношения
. Существование пределов следует из монотонности и ограниченности. Равенства из соотношения  Отметим еще, что функция распределения имеет не более, чем счетное число скачков. (Число
Отметим еще, что функция распределения имеет не более, чем счетное число скачков. (Число  скачков размером не более
скачков размером не более  ограничено величиной
ограничено величиной  ). Функция, удовлетворяющая условиям 1-6 является ф-ией распределения(некоторой случайной величины). Однако, из равенства
). Функция, удовлетворяющая условиям 1-6 является ф-ией распределения(некоторой случайной величины). Однако, из равенства  не следует совпадения
не следует совпадения  ; они могут различаться с вероятностью единица.
; они могут различаться с вероятностью единица.
39. Формулы Байеса В ряде случаев приходится рассматривать вероятности событий при дополнительном условии, что произошло некоторое событие В. Такие вероятности мы будем называть условными и обозначать символом  ; это означает вероятность события А при условии, что В произошло.
; это означает вероятность события А при условии, что В произошло. 
 , если известно, что В произошло. Согласно теореме умножения имеем:
, если известно, что В произошло. Согласно теореме умножения имеем: 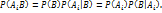 Отсюда
Отсюда  используя формулу полной вероятности, находим, что
используя формулу полной вероятности, находим, что 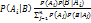 Полученные нами формулы носят название формул Байеса.
Полученные нами формулы носят название формул Байеса.
41.Центральная предельная теорема. Теорема(Леви):Пусть  последовательность независимых одинаково распределенных случайных величин (мат. ожидания одинаковые).
последовательность независимых одинаково распределенных случайных величин (мат. ожидания одинаковые).
 , тогда
, тогда  (слабая сходимость). 𝒫 – вероятностное распределение.
(слабая сходимость). 𝒫 – вероятностное распределение.  - случайная величина;
- случайная величина; 
Дата добавления: 2015-04-11; просмотров: 97 | Поможем написать вашу работу | Нарушение авторских прав |