
Читайте также:
|
Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.Из свойства симметрии пространства – его однородности следуетзакон сохранения импульса.
Однородность времени означает инвариантность физических законов относительно выбора начала отсчета времени. Например, при свободном падении тела в поле силы тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать. Из однородности времени следует закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Изотропность пространства означает инвариантность физических законов относительно выбора направлении осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). Из изотропности пространства следует фундаментальный закон природы – закоя сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
4. Система отсчёта — это совокупность точки отсчёта, системы координат и системы отсчёта времени, связанных с этой точкой, по отношению к которой изучается движение (или равновесие) каких-либо других материальных точек или тел.
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся.
Свойства ИСО: 1) Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО.
2) Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.
3) Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
Неинерциа́льная систе́ма отсчёта — произвольная система отсчёта, не являющаяся инерциальной. Примеры неинерциальных систем отсчета: система, движущаяся прямолинейно с постоянным ускорением, а также вращающаяся система.
При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.
Основное уравнение динамики относительного движения материальной точки имеет вид:
 ,
,
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Синхрониза́ция часов — процесс приведения к одному значению одного параметра разных объектов, называемого временем.
Преобразование декартовых координат при параллельном сдвиге осей определяется формулами:
 ,
,  ,
,  ,
,  .
.
5. Перемеще́ние — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).
Можно определить перемещение, как изменение радиус-вектора точки:  .
.
Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора  этой точки:
этой точки:

Ускоре́ние — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
 .
.
Основной задачей кинематики является определение закона движения тела, или другими словами, определение местоположения его в пространстве в определенный момент времени. Обратная задача кинематики – определение кинематических характеристик (скорости, ускорения) по известному закону движения.
6. Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Величина, обратная кривизне кривой (r = 1 / κ), называется радиусом кривизны; он совпадает с радиусом соприкасающейся окружности в данной точке кривой. Центр этой окружности называется центром кривизны.
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости.
Величину тангенциального ускорения - в смысле проекции вектора ускорения на единичный касательный вектор траектории - можно выразить так: 
Центростремительное ускорение (нормальное) — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. Такое ускорение направлено к центру кривизны траектории, чем и обусловлен термин.
 ,
, 
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени: 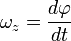 ,
,
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно: 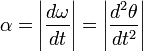 .
.
7. Преобразова́ния Галиле́я — в классической механике преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея).
Если ИСО S движется относительно ИСО S' с постоянной скоростью 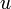 вдоль оси
вдоль оси  , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:
, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: 
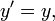

 или, используя векторные обозначения,
или, используя векторные обозначения, 
 .
.
Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета: 
 .
.
Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть  , то ускорение
, то ускорение  тела относительно обеих систем отсчета одинаково.
тела относительно обеих систем отсчета одинаково.
Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея.
 ,
,  ,
, 

Если  то средние скорости совпадают с мгновенными
то средние скорости совпадают с мгновенными  или короче
или короче 
— как для средних, так и для мгновенных скоростей (формула сложения скоростей).
8. И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:  .
.
Ма́сса — одна из важнейших физических величин. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя).
Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.
Инертная масса, которая характеризует меру инертности тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
Опыт Этвеша: Опыт ставился следующим образом. На нити подвешивался стержень с 2 грузами на краях: из меди и платины. Стержень ориентировался перпендикулярно к меридиану. Плечи стержня равны. Грузы по весу равны. Если бы массы не были равны, то направление отвеса зависело бы от материала, из которого сделан шар отвеса. Однако Этвеш с помощью этих крутильных весов установил, что отвес не меняет своего направления независимо от материала, из которого от изготовлен. Таким образом, устанавливалось равенство гравитационной и инертной масс.
9. Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.
Силу измеряют посредством динамометров, силоизмерительных машин и прессов, а также нагружением при помощи грузов и гирь.
10. Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

Третий закон Ньютона объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой  , а второе — на первое с силой
, а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
11. В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором  , определяемым как
, определяемым как  где
где  – масса и радиус-вектор
– масса и радиус-вектор  -й частицы,
-й частицы,  – масса всей системы,
– масса всей системы,  – полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на
– полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на  , то получится:
, то получится:  или
или  , где
, где  – скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:
– скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:  .
.
Центр масс в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:  .
.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
12. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:  .
.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело  .
.
Момент силы — производная по времени от момента импульса  , где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
, где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.  . То есть если I постоянная, то
. То есть если I постоянная, то  .
.
13. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы:  ,
,  .
.
Внешние силы это активно приложенные нагрузки - силы и моменты. Бывают временные и постоянные. Приложенная нагрузка может создаваться в результате активного воздействия на тело окружающей среды. К внешним нагрузкам относят также реакции. Эти нагрузки прикладываются к нагруженным элементам со стороны сопрягающихся с ними опор, например, сила противодействия пилоту со стороны рычага, нагрузка на вал со стороны подшипников, силы и моменты со стороны фюзеляжа на крыло или на стойку шасси и т.д.
По характеру действия силовые факторы подразделяются на статичес-кие и динамические нагрузки.
Статические нагрузки - силы и моменты постоянные или медленно изменяющиеся по величине
Динамические нагрузки - силы и моменты, которые прикладываются внезапно, сразу полной своей величиной - ударные, быстро нарастают либо убывают - инерционные, изменяются по направлению - циклические.
По способу приложения силовые факторы подразделяются на сосредоточенные и распределенные.
Сосредоточенными силами называются силы, передающиеся на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента.
Распределенными силами называют силы, приложенные к элементам конструкции на протяжении некоторой длины или площади, могут быть равномерно распределенными или неравномерно распределенными.
Вес горизонтально расположенной балки представляет собой нагрузку, равномерно распределенную по длине (погонную нагрузку).
14. Тре́ние — процесс взаимодействия твёрдых тел при их относительном движении (смещении) либо при движении твёрдого тела в газообразной или жидкой среде.
Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
Сухое трение — когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твердыми смазочными материалами) — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.
Жидкостное трение — при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды.
15. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного ивращательного движения.
Если система замкнута, то есть 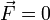 , то
, то 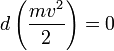 , а величина
, а величина  остаётся постоянной. Эта величина называется кинетической энергией частицы.
остаётся постоянной. Эта величина называется кинетической энергией частицы.
Потенциальная энергия  — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.
— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.
Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.
Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.
Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: Ep = mgh.
16. Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
С фундаментальной точки зрения, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система.
Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства.
18. В некоторых случаях тел связано с изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п.
Произведем вывод уравнения движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за промежуток времени dt

где u - скорость истечения газов относительно ракеты. Тогда  здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому
здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому  или
или 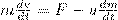 (1)
(1)
Второе слагаемое в правой части называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы  которое впервые было выведено И. В. Мещерским.
которое впервые было выведено И. В. Мещерским.
 откуда
откуда  Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени стартовая масса m0, а ее скорость ракеты равна нулю, то С = uln(m0). Следовательно,
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени стартовая масса m0, а ее скорость ракеты равна нулю, то С = uln(m0). Следовательно, 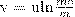 . Это соотношение называется формулой Циолковского.
. Это соотношение называется формулой Циолковского.
19.Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета:  , где
, где  — сила, действующая на тело со стороны других тел;
— сила, действующая на тело со стороны других тел;
 — сила инерции, действующая на тело относительно поступательно движущейся НСО.
— сила инерции, действующая на тело относительно поступательно движущейся НСО.  — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
— ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;  — центробежная сила инерции, действующая на тело относительно вращающейся НСО.
— центробежная сила инерции, действующая на тело относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО,
— угловая скорость НСО относительно ИСО,  — расстояние от тела до центра вращения;
— расстояние от тела до центра вращения;
 — кориолисова сила инерции, действующая на тело, движущееся со скоростью
— кориолисова сила инерции, действующая на тело, движущееся со скоростью  относительно вращающейся НСО.
относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
— угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
Силы инерции при ускоренном поступательном движении системы отсчета. На тележке к штативу на нити подвешен шарик массой m (рис. 1). Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции (натяжения) нити Т. Если тележку привести в поступательное движение с ускорением а 0, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла α, пока результирующая сила F = P + T не даст ускорение шарика, равное а 0. Значит, результирующая сила F направлена в сторону ускорения тележки а 0 и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением а 0) равна F=mgtgα=ma0, откуда  т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки.
т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки.
В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F in, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,  (2)
(2)
Проявление сил инерции при поступательном движении мы можем видеть в повседневных явлениях. Если поезд набирает скорость, то пассажир, сидящий при этом по ходу поезда, прижимается к спинке сиденья под действием силы инерции. Наоборот, при торможении поезда пассажир отклоняется от спинки сиденья, т.к. сила инерции направлена в противоположную сторону. Особенно силы инерции заметны при внезапном торможении поезда. Эти силы проявляются в перегрузках, возникающие при запуске и торможении космических кораблей.
На практике действие центробежных сил инерции испытывают, например, пассажиры в движущемся автобусе на поворотах, летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах и т. д., где они достигают очень больших значений. При проектировании быстро вращающихся деталей машин (винтов самолетов, роторов и т. д.) используются специальные механизмы для уравновешивания центробежных сил инерции.
Центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью.
Сила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета, чаще всего рассматривается случай относительно Земли. Действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север, то действующая на него сила Кориолиса будет направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д. Также можно показать, что в южном полушарии сила Кориолиса, которая действует на движущиеся тела, направлена влево по отношению к направлению движения.
20. При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Предполагается, что за время удара действием внешних сил можно пренебречь, тогда полный импульс тел при ударе сохраняется, в противном случае нужно учитывать импульс внешних сил.
Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара. Обычно рассматривают либо абсолютно упругий удар, либо вводят коэффициент сохранения энергии k, как отношение кинетической энергии после удара к кинетической энергии до удара при ударе одного тела о неподвижную стенку, сделанную из материала другого тела.
Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Абсолю́тно неупру́гий удар —удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Энергия, конечно же, никуда не исчезает, а переходит в тепловую.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
21. Первый закон Кеплера: Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением  , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
, где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
Второй закон Кеплера: Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
Третий закон Кеплера: Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.  , где T 1 и T 2 — периоды обращения двух планет вокруг Солнца, а a 1 и a 2 — длины больших полуосей их орбит.
, где T 1 и T 2 — периоды обращения двух планет вокруг Солнца, а a 1 и a 2 — длины больших полуосей их орбит.
Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:  , где M — масса Солнца, а m 1 и m 2 — массы планет.
, где M — масса Солнца, а m 1 и m 2 — массы планет.
Закон тяготения Ньютона гласит, что сила гравитационного притяжения между двумя материальными точками массы m и M, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:  . Здесь G — гравитационная постоянная, равная примерно 6,6725×10-11 м³/(кг·с²).
. Здесь G — гравитационная постоянная, равная примерно 6,6725×10-11 м³/(кг·с²).
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением.
Для двух тяготеющих точечных тел с массами M и m гравитационная энергия Ug равна:  .
.
22. Требовалось экспериментально доказать справедливость закона всемирного тяготения и для обычных тел. Именно это и сделал Г.Кавендиш, попутно определив среднюю плотность Земли:  ,
,  .
.
Установка представляет собой деревянное коромысло с прикреплёнными к его концам небольшими свинцовыми шарами диаметром 5 см и массой 775 г. Оно подвешено на нити из посеребрённой меди длиной 1 м. К шарам подносят шары большего размера диаметром 20 см и массой 49,5 кг, сделанные также из свинца. В результате действия гравитационных сил коромысло закручивается на некий угол. Жёсткость нити была такой, что коромысло делало одно колебание за 15 минут. Угол поворота коромысла определялся с помощью луча света, пущенного на зеркальце на коромысле, и отражённого в микроскоп. Зная упругие свойства нити, а также угол поворота коромысла, можно вычислить гравитационную постоянную.
Для предотвращения конвекционных потоков установка была заключена в ветрозащитную камеру. Угол отклонения измерялся при помощи телескопа.
Заподозрив в качестве причины закручивания нити магнитное взаимодействие железного стержня и свинцовых шаров, Кавендиш заменил стержень медным, получив те же результаты.
23. Вес — сила воздействия тела на опору (или другой вид крепления в случае подвешенных тел), препятствующую падению, возникающая в поле сил тяжести. Вес в инерциальной системе отсчёта  совпадает с силой тяжести и пропорционален массе
совпадает с силой тяжести и пропорционален массе  и ускорению свободного падения
и ускорению свободного падения  в данной точке:
в данной точке: 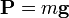 .
.
При движении системы тело — опора (или подвес) относительно инерциальной системы отсчёта c ускорением  вес перестаёт совпадать с силой тяжести:
вес перестаёт совпадать с силой тяжести:  .
.
Весы́ — устройство или прибор для определения массы тел (взвешивания) по действующему на них весу, приближённо считая его равным силе тяжести.
24. Невесо́мость — состояние, при котором сила взаимодействия тела с опорой (вес тела), возникающая в связи с гравитационным притяжением, действием других массовых сил, в частности силы инерции, возникающей при ускоренном движении тела, отсутствует. Для понимания сути невесомости можно рассмотреть летящий по баллистической траектории самолёт. Такие применяются для тренировки космонавтов в России и США. В кабине пилота на нитке подвешен грузик, который обычно натягивает нитку вниз (если самолет покоится либо движется равномерно и прямолинейно). Когда нить, на которой висит шарик не натянута, имеет место состояние невесомости. Таким образом, пилот должен управлять самолётом так, чтобы шарик висел в воздухе, а нить не была натянута. Для достижения этого эффекта самолёт должен иметь постоянное ускорение g, направленное вниз. Другими словами, пилоты создают нулевую перегрузку. Длительно такую перегрузку (до 40 секунд) можно создать, если выполнить специальную фигуру пилотажа (которая не имеет названия). Траектория такой фигуры напоминает петлю Нестерова, в которой, как известно, перегрузка направлена к центру петли.
Принцип эквивалентности сил гравитации и инерции — эвристический принцип, использованный Альбертом Эйнштейном при выводе общей теории относительности. Один из вариантов его изложения: «Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное тело — гравитационная или сила инерции».
Для доказательства этого принципа Эйнштейн предложил следующий мысленный эксперимент. Пусть тела находятся в лифте, который бесконечно удалён от гравитирующих тел и двигается с ускорением. Тогда на все тела, находящиеся в лифте действует сила инерции  , а тела под действием этих сил будут давить на опору или подвес. То есть тела будут обладать весом.
, а тела под действием этих сил будут давить на опору или подвес. То есть тела будут обладать весом.
Если лифт не движется, а висит над какой-то гравитирующей массой в однородном поле, то все тела также будут обладать весом. Находясь в лифте, невозможно отличить эти две силы. Поэтому все механические явления будут в обоих лифтах происходить одинаково. Эйнштейн обобщил это положение на все физические явления.
25. В основе ряда опытов, демонстрирующих вращение Земли, используется эффект Саньяка: если кольцевой интерферометр совершает вращательное движение, то вследствие релятивистских эффектов полосы смещаются на угол  , где A — площадь кольца, c — скорость света, ω — угловая скорость вращения.
, где A — площадь кольца, c — скорость света, ω — угловая скорость вращения.
Впервые публичная демонстрация была осуществлена французским физиком и астрономом Жаком Фуко в 1851 г. в Парижском Пантеоне. Под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м, крепление маятника позволяло ему свободно колебаться во всех направлениях, под точкой крепления было сделано круговое ограждение диаметром 6 метров, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли.
Период колебания маятника при такой длине подвеса составлял 16,4 секунд, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло ~3 мм, за час плоскость колебаний маятника повернулась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершила полный оборот и вернулась в прежнее положение.
Маятник Фуко является математическим маятником, такой маятник, отклонённый от равновесного положения, совершает колебания в плоскости, неподвижной в инерциальной системе отсчёта (в данном случае — системе отсчёта, «связанной» со звёздами) и проявляет, таким образом, свойства гироскопа. Наблюдатель, находящийся на Земле и вращающийся вместе с нею, находится в неинерциальной (вращающейся) системе отсчёта и будет видеть, что плоскость колебаний маятника медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.
Скорость вращения плоскости колебаний идеального маятника Фуко Ω P (в градусах в звёздный час) относительно поверхности Земли составляет  Для неидеального маятника Фуко скорость вращения плоскости колебаний зависит и от длины подвеса:
Для неидеального маятника Фуко скорость вращения плоскости колебаний зависит и от длины подвеса:  где
где  — амплитуда колебаний груза маятника;
— амплитуда колебаний груза маятника;  — длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса.
— длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса.
Тело свободно падает в поле тяжести Земли: F = 0 a = g + 2 [ V, w ].
При падении свободно падающих тел без начальной скорости кориолисова сила проявляется в отклонении свободно падющих тел к востоку и экватору от направления отвеса.
Метод последовательных приближений: 2 [ V, w ] мал по сравнению с g. Отбросим в нулевом приближении a = g V = V (o) + g t
Подставим V из нулевого приближения: a = g + 2 [ V (o), w ] + 2 t[ g, w ], V = V (o) + g t + 2t [ V (o), w ] + t^2[ g, w ] a = g + 2 [ V (o), w ] + 2t [ g, w ] + 4t [[ V (o), w ], w ] + 2 * t^2 [[ g, w ], w ],
V = V (o) + g t + 2t [ V (o), w ] + t^2[ g, w ] + 2t^2[[ V (o), w ], w ] + 2/5 t^3 [[ g, w ], w ]
r = r (o) + V (o)t + 1/2 g t^2 + t^2 [ V (o), w ] + 1/3 t^3 [ g, w ] + 2/3 t^3 [[ V (o), w ], w ] + 1/6 t^4 [[ g, w ], w ]
Если V(o) = 0: S = r - r (o), S = 1/2 g t^2 + 1/3 t^3 [ g, w ]+ 1/6 t^4 [[ g, w ], w ].
Ось х - на восток; ось у - к экватору по меридиану; ось z - по отвесу вниз: z = 1/2 g t^2 - 1/6 w^2 t^4 g cos^2(θ)
x Ξ S(восп) = 1/3 w t^3 g cos (θ)
у Ξ S(экв) = 1/12 w^2 t^4 g sin(2 θ)
S(вопс) = 2/3 w t h cos(θ) = 4/3 п t/T h cos (θ), h - высота падения. T = 2п/w - период суточного вращения Земли.
S(экв) = w t sin(θ)/2 S(вост) – очень мало.
26. Степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел.
Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных.
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Заметим, что при этом оно не обязательно является прямолинейным.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела положением любых двух точек.
Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве.
Углы Эйлера определяют три поворота системы, которые позволяют привести любое положение системы к текущему. Обозначим начальную систему координат как (x, y, z), конечную как (X, Y, Z). Пересечение координатных плоскостей xy и XY называется линией узлов N.
Угол α между осью x и линией узлов.
Угол β между осями z и Z.
Угол γ между осью X и линией узлов.
Повороты системы на эти углы называются прецессия, нутация и поворот на собственный угол (вращение). Такие повороты некоммутативны и конечное положение системы зависит от порядка, в котором совершаются повороты. В случае углов Эйлера это последовательность 3,1,3 (Z,X,Z).
27. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Тензор инерции — в механике абсолютно твёрдого тела — величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью:  .
.
в компонентах это выглядит так:  ,
,  .
.
Как и любой симметричный тензор, тензор инерции может быть диагонализован, то есть можно найти три ортогональные оси координат (собственные оси, орты которых являются собственными векторами и образуют собственный базис тензора инерции) — жестко связанные, конечно, с твёрдым телом, — в которых матрица тензора инерции диагональна, и её собственные числа (собственные числа тензора инерции) определяют главные моменты инерции тела.
Нетрудно видеть, что главные моменты инерции совпадают с осевыми моментами инерции относительно главных осей:
 ,
,
 ,
,
 ,
,
Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями: 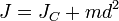 .
.
29. Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Для однородного цилиндра одной из главных осей инерции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоскости, перпендикулярной геометрической оси цилиндра. Главными осями инерции шар являются любые три взаимно перпендикулярные оси, проходящие через центр масс.
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения.
Можно показать, что вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым.
Если, например, палочку подвесить за один конец нити, а другой конец, закрепленный к шпинделю центробежной машины, привести в быстрое вращение, то палочка будет вращаться в горизонтальной плоскости около вертикальной оси, перпендикулярной оси палочки и проходящей через ее середину (рис.31). Это и есть свободная ось вращения (момент инерции при этом положении палочки максимальный). Если теперь палочку, вращающуюся вокруг свободной оси, освободить от внешних связей (аккуратно снять верхний конец нити с крючка шпинделя), то положение оси вращения в пространстве в течение некоторого времени сохраняется. Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью.
30. Гироскоп обладает следующими характерными свойствами: 1) Сохраняет положение оси вращения в пространстве
2) Устойчив к ударным воздействиям;
3) Обладает необычной реакцией на действие внешней силы (если сила стремится повернуть гироскоп относительно одной оси, то он поворачивается вокруг другой, ей перпендикулярной);
4) Безынерционен.
Нутация - происходящее одновременно с прецессией движение твёрдого тела, при котором изменяется угол между осью собственного вращения тела и осью, вокруг которой происходит прецессия; этот угол называется углом нутации.
Чистая нутация — это такое движение оси вращения, при котором первый угол Эйлера остаётся постоянным.
Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы.Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Главное свойство прецессии — безинерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве.
31. Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Для тонкого растяжимого стержня закон Гука имеет вид:  .
.
Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как  .
.
В общем случае напряжение и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга Cijkl и содержит 81 коэффициент. Вследствие симметрии тензора Cijkl, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
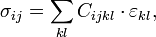 где σ ij — тензор напряжений, ε kl, — тензор деформаций. Для изотропного материала тензор Cijkl содержит только два независимых коэффициента.
где σ ij — тензор напряжений, ε kl, — тензор деформаций. Для изотропного материала тензор Cijkl содержит только два независимых коэффициента.
В теории упругости явление гистерезиса наблюдается в поведении упругих материалов, которые под воздействием больших давлений способны сохранять деформацию и утрачивать её при воздействии обратного давления (например, вытягивание сжатого стержня). Во многом именно это явление объясняет анизотропию механических характеристик кованых изделий, а также их высокие механические качества.
Различают два вида упругого гистерезиса — динамический и статический.
Динамический гистерезис наблюдают при циклически изменяющихся напряжениях, максимальная амплитуда которых существенно ниже предела упругости. Причиной этого вида гистерезиса является неупругость либо вязкоупругость. При неупругости, помимо чисто упругой деформации (отвечающей закону Гука), имеется составляющая, которая полностью исчезает при снятии напряжений, но с некоторым запаздыванием, а при вязкоупругости эта составляющая со временем исчезает не полностью. Как при неупругом, так и вязкоупругом поведении величина Δ U — энергия упругой деформации — не зависит от амплитуды деформации и меняется с частотой изменения нагрузки. Также динамический гистерезис возникает в результате термоупругости, магнитоупругих явлений и изменения положения точечных дефектов и растворённых атомов в кристаллической решётке тела под влиянием приложенных напряжений.
Растяжение-сжатие — вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс).
Сдвиг — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно).
Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым.
Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил(момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор —крутящий момент. На кручение работают пружины растяжения-сжатия и валы.
32. Модуль Юнга (модуль упругости) — коэффициент, характеризующий сопротивление материала растяжению/сжатию при упругой деформации. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса.

Модулем сдвига (обозначается буквой G или μ), называется отношение касательного напряжения к сдвиговой деформации  где
где  — касательное напряжение; F — действующая сила; A — площадь, на которую действует сила;
— касательное напряжение; F — действующая сила; A — площадь, на которую действует сила;  — сдвиговая деформация; Δ x — смещение; I — начальная длина.
— сдвиговая деформация; Δ x — смещение; I — начальная длина.
Модуль сдвига связан с модулем Юнга через коэффициент Пуассона:  .
.
Дата добавления: 2015-01-30; просмотров: 89 | Поможем написать вашу работу | Нарушение авторских прав |