Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.

Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному

вектору.

Пусть плоскость задана точкой M₀(x₀;y₀;z₀

) и вектором ,

перпендикулярной этой плоскости.

Возьмем произвольную точку M(x;y;z) и составим вектор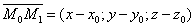

. При любом расположении точки М на плоскости Q

, поэтому .

Общее уравнение плоскости.

· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)

· Если С=0 то вектор

. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.

· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0.

· Если А=В=0 то уравнение примет вид плоскость параллельна плоскости Oxy.

· Если A=B=D=0, то уравнение имеет вид . Это уравнение плоскости Oxy.

Уравнение плоскости, проходящей через три точки

К (х₁;у₁) М (х₂;у₂) N (x₃;y₃)

Возьмем на плоскости точку P (x;y;z).

Составим векторы:

Эти векторы лежат в одной плоскости, следовательно они компланарны:

Уравнение плоскости в отрезках.

Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:

; ;

Нормальное уравнение плоскости.