Читайте также:
|
Математическое программирование — дисциплина, изучающая теорию и методы решения задачи оптимизации.
Математическое программирование - раздел математики, исследующий математические модели и методы решения многоэкстремальных задач с ограничениями.
Задачи математического программирования подразделяются на:
- выпуклые: линейное и выпуклое программирование;
- динамические: динамическое программирование;
- сетевые;
- дискретные: решение в целых числах; и
- стохастические: стохастическое программирование.
Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений. В самом общем виде задача записывается так:
U = f(x) → max; x ∈ M,
где x = (x1, x2,..., xn); M — область допустимых значений переменных x1,..., xn; f(x) — целевая функция.
Частный случай задачи М. п. — “классическая задача”. В ней область M представлена равенствами:
g (x) = b,
где g(x) — вектор функций ограничений; b — вектор констант ограничений.
Названные выше разнообразные дисциплины отличаются друг от друга видом целевой функции f(x) и области М. Напр., если f(x) линейна, а М — выпуклый многогранник, имеем задачу линейного программирования; если же дополнительно ставится условие, чтобы переменные были целочисленными, то имеем задачу целочисленного программирования; если зависимость U от x (т. е. форма f) носит нелинейный характер, то задачу нелинейного программирования.
Развивающаяся область — стохастическое программирование, задачи которого в отличие от детерминированных задач характеризуются тем, что их исходные данные (все или часть) — суть случайные величины.
Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Задачами нелинейного программирования называются задачи мат.программирования, в которых нелинейны и (или) целевая функция и (или) ограничения в виде неравенств или равенств. На практике возникают довольно часто. Многие такие задачи могут быть приближены к задачам линейного программирования. Мощным средством решения задач нелинейного программирования являются численные методы. Они позволяют найти решение задачи с заданной степенью точности.
Общий вид записи:
Найти переменные 
, удовлетворяющие системе уравнений:
V()= 
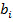i=1, 2..m
И обращающие в максимум (минимум) целевую функцию Z=f().
Динамическое программирование – это вычислительный метод для решения задач определенной структуры. Динамическое программирование представляет собой направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму.
Свойства задач для этого метода:
- задача должна допускать интерпретацию как n-шаговый процесс принятия решений.
- задача должна быть определена для любого числа шагов и иметь структуру, не зависящую от их числа
-должно быть заданное некоторое множество параметров, которое описывает состояние системы, от которых зависят оптимальные решения переменных
- выбор решения на k-м шаге не должен оказывать влияния на предыдущие решения, кроме необходимого пересчета переменных.
Пример: задача о выборе траектории, задача последовательного принятия решений.
Теория графов: Графом G=(V,E) (или G=(p,q)) называется пара множеств, где V – непустое, конечное множество, состоящее из р элементов (вершин графа G), E – множество неупорядоченных пар элементов q (ребра).
Отрезки, соединяющие вершины, называются дугами, если указано, какая вершина является начальной, и ребрами, если ориентация не указана.
Граф, состоящий из дуг, называется ориентированным (оргрфом). Граф образованный ребрами – неориентированный.
Если Е – пустое множество, то граф G – пустой граф.
Мультиграф – между двумя вершинами можно нарисовать 2 и более ребра.
Если имеются вершины V1 и V2 и ребро е образовано ими, то говорят, что ребро е инцидентно вершинам V1 и V2. V1 и V2 – смежные.
Степенью вершины называется число ребер инцидентных данной вершине (количество выходящих из нее ребер).
Вершина, степень которой равна 1, называется висящей.
Вершина, степень которой равна 0, называется изолированной.
Последовательность ребер V0, V1… называется маршрутом.
Если в маршруте не указаны ребра, то такой маршрут называется цепью.
Если V0=Vn, то цепь называют циклом.
Если в цепи не повторяются вершины, то такая цепь называется простой.
Граф называется связным, если любая пара его вершин соединена маршрутом.
Если в связном графе имеется цикл, проходящий через все ребра графа, то граф называется Эйлеровым.
Связный граф, не имеющий циклов – дерево.
Дата добавления: 2015-04-20; просмотров: 120 | Поможем написать вашу работу | Нарушение авторских прав |