
Читайте также:
|




Рис. 1. Агрегатированная модель транспортной сети г. Ржев
Для расчета кратчайших расстояний между вершинами транспортной сети используем метод потенциалов.
Принимаем вершину 1 за начальную. Её потенциал равен нулю.
1-2. 0+3,1=3,1
1-3. 3,1+3,9=7
1-4. 3,1+5,8=8,9
1-5. 7+3,1=10,1
1-6. 10,1+3,1=13,2
1-7. 7+5,8=12,8
1-8. 12,8+3,1=15,9
1-9. 13,2+3,4=16,6
1-10. 15,9+3,3=19,2
1-11. 16,6+3,7=20,3
1-12. 20,3+4,1=24,4
1-13. 20,3+5,1=25,4
1-14. 25,4+3,2=28,6
1-15. 25,4+3,6=29
1-16. 24,4+3,4+4=31,8
1-17. 24,4+3,4=27,8
1-18. 27,8+3,1=30,9
Расчет кратчайших расстояний до всех остальных пунктов производится аналогично. Результаты расчета представлены в таблице 1.
Таблица 1
Матрица кратчайших расстояний
| Из | В вершину | |||||||||||||||||
| Х | 3,1 | 8,9 | 10,1 | 13,2 | 12,8 | 15,9 | 16,6 | 19,2 | 20,3 | 24,4 | 25,4 | 28,6 | 31,8 | 27,8 | 30,9 | |||
| 3,1 | Х | 3,9 | 5,8 | 10,1 | 9,7 | 12,8 | 13,5 | 16,1 | 17,2 | 21,3 | 22,3 | 25,5 | 25,9 | 28,7 | 24,7 | 27,8 | ||
| 3,9 | Х | 3,5 | 3,1 | 6,2 | 5,8 | 8,9 | 9,6 | 12,2 | 13,3 | 17,4 | 18,4 | 21,6 | 24,8 | 20,8 | 23,6 | |||
| 8,9 | 5,8 | 3,5 | Х | 3,4 | 6,5 | 10,1 | 9,9 | 13,4 | 13,6 | 17,7 | 18,7 | 21,9 | 22,3 | 25,1 | 21,1 | 24,2 | ||
| 10,1 | 3,1 | 3,4 | Х | 3,1 | 3,6 | 6,7 | 6,5 | 10,2 | 14,3 | 15,3 | 18,5 | 18,9 | 21,7 | 17,7 | 20,8 | |||
| 13,2 | 10,1 | 6,2 | 6,5 | 3,1 | Х | 4,1 | 7,2 | 3,4 | 5,3 | 9,4 | 10,4 | 13,6 | 16,8 | 12,8 | 15,9 | |||
| 12,8 | 9,7 | 5,8 | 3,6 | 4,1 | Х | 3,1 | 4,9 | 6,4 | 8,6 | 12,7 | 13,7 | 16,9 | 17,3 | 20,1 | 16,1 | 19,2 | ||
| 15,9 | 12.8 | 8.9 | 10.1 | 6.7 | 7.2 | 3.1 | X | 3.9 | 3.3 | 7.6 | 11.7 | 12.7 | 15.9 | 16.3 | 19.1 | 15.1 | 18.2 | |
| 16.6 | 13.5 | 9.6 | 9.9 | 6.5 | 3.4 | 4.9 | 3.9 | Х | 4.6 | 3.7 | 7.8 | 8.8 | 12.4 | 15.2 | 11.2 | 14.3 | ||
| 19.2 | 16.1 | 12.2 | 13.4 | 6.4 | 3.3 | 4.6 | Х | 8.3 | 12.4 | 13.4 | 16.6 | 19.8 | 15.8 | 18.9 | ||||
| 20,3 | 17,2 | 13,3 | 13,6 | 10,2 | 5,3 | 8,6 | 7,6 | 3,7 | 8,3 | Х | 4,1 | 5,1 | 8,3 | 8,7 | 11,5 | 7,5 | 10,6 | |
| Продолжение таблицы 1 | ||||||||||||||||||
| 24,4 | 21,3 | 17,4 | 17,7 | 14,3 | 9,1 | 12,7 | 11,7 | 7,8 | 12,4 | 4,1 | Х | 3,4 | 6,6 | 6,3 | 7,4 | 3,4 | 6,5 | |
| 25,4 | 22,3 | 18,4 | 18,7 | 15,3 | 10,4 | 13,7 | 12,7 | 8,8 | 13,4 | 5,1 | 3,4 | Х | 3,2 | 3,6 | 10,5 | 6,5 | 9,6 | |
| 28,6 | 25,5 | 21,6 | 21,9 | 18,5 | 13,6 | 16,9 | 15,9 | 16,6 | 8,3 | 6,6 | 3,2 | Х | 4,2 | 11,1 | 7,1 | 10,2 | ||
| 25,9 | 22,3 | 18,9 | 17,3 | 16,3 | 12,4 | 8,7 | 6,3 | 3,6 | 4,2 | Х | 6,9 | 2,9 | ||||||
| 31,8 | 28,7 | 24,8 | 25,1 | 21,7 | 16,8 | 20,1 | 19,1 | 15,2 | 19,8 | 11,5 | 7,4 | 10,5 | 11,1 | 6,9 | Х | 6,1 | ||
| 27,8 | 24,7 | 20,8 | 21,1 | 17,7 | 12,8 | 16,1 | 15,1 | 11,2 | 15,8 | 7,5 | 3,4 | 6,5 | 7,1 | 2,9 | Х | 3,1 | ||
| 30,9 | 27,8 | 23,6 | 24,2 | 20,8 | 15,9 | 19,2 | 18,2 | 14,3 | 18,9 | 10,6 | 6,5 | 9,6 | 10,2 | 6,1 | 3,1 | Х |
Децентрализованный вариант организации перевозок
Определяется суммарное количество ездок всех автомобилей на маршруте, необходимое для перевозки заявленного количества груза:
 ,
,
где Qсут – объем перевозок груза (по заявке); q - грузоподъемность автомобиля.
Далее определяется время оборота одного автомобиля:
Тоб. = 2t езд + t пог./раз.
Время ездки составляет:

Определятся время на выполнение нулевых пробегов: первый нулевой пробег согласно заявке от АТП до склада, второй нулевой пробег от строительного объекта до АТП.
Далее определяется количество ездок выполненных за смену:

Определяется необходимое количество автомобилей для перевозки груза по заявке:
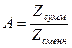
Определяется пробег всех автомобилей с грузом:
Lгр = Lезд. * Zсмен. * А
Пробег всех автомобилей без груза составляет:
Lпор. = (Lезд. * (Zсмен. – 1) + Lнул.1 + Lнул.2) * А
Коэффициент использования пробега:

Время работы на маршруте определяется:
Траб. = Тоб. * Zсмен. + tнул1 + tнул2 - t хол
Остаток времени в наряде:
Тост. = Тнар.- Траб.
Дата добавления: 2015-09-11; просмотров: 179 | Поможем написать вашу работу | Нарушение авторских прав |