
Читайте также:
|
Пусть f(x,y) — функция двух переменных x, у, определенная в некоторой окрестности точки (хо, уо). Если существует конечный предел

то говорят, что функция f\x,y) имеет в точке (хо, уо) частную производную по переменной x. Аналогично определяется частная производная по у. Обозначают


Пусть f(x), x = (x1, x2, …, xn) Î G Ì Rn — функция п переменных, определенная в области G п -мерного пространства Rn.
Частной производной функции f(x1, x2, …, xn) по переменной x, называется конечный предел
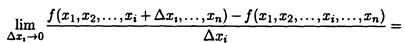

Обозначаем

Для приращения дифференцируемой функции f(x1, x2, …, xn) справедливо равенство
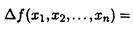


Если в пространстве Rn задан единичный вектор


то изменение дифференцируемой функции f(x) в направлении l характеризуется производной по направлению:
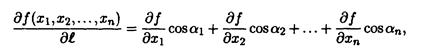

где (grad f, l) — скалярное произведение вектора

на вектор направления l
Поскольку —  , где j — угол между векторами grad f и l, то вектор grad f указывает направление наискорейшего возрастания функции f(x).
, где j — угол между векторами grad f и l, то вектор grad f указывает направление наискорейшего возрастания функции f(x).
Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим частные производные второго порядка:
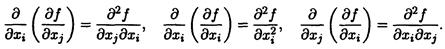
Если смешанные производные  и
и  непрерывны, то их значения не зависят от порядка дифференцирования.
непрерывны, то их значения не зависят от порядка дифференцирования.
Аналогично определяются производные более высоких порядков:

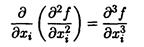
Дата добавления: 2015-09-10; просмотров: 73 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Линии уровня. Локальные экстремумы. | | | ГЛАВА ПЕРВАЯ |