Читайте также:
|
Рассмотрим переменную величину xn=(1+1/n)n, где n =1,2,3…. Можно доказать, что xn=(1+1/n)n возрастает и 2<(1+1/n)n<3, то есть эта последовательность имеет конечный предел. Этот предел обозначается ‘e’.
Определение. Предел переменной величины (1+1/n)n при n→∞ называется числом е
. (7)
Это число е = 2,7182818284…
Мы рассмотрели последовательность (1+1/n)n, n= 1,2,3… При непрерывном изменении переменной х и если х→∞, то 
и 
. То есть получаем, что
. (8)
Этот предел называется вторым замечательным пределом.
Второй замечательный предел можно записать в виде
. (9)
Число е – иррациональное число, оно играет очень важную роль в математическом анализе.
Мы рассматривали логарифмическую функцию у=logax, а ≠ 1, а > 0, а – основание логарифма. Если основанием логарифма является е, то logex = ln x и называется натуральным логарифмом. Функция у = ех называется экспонентой.
Примеры: 
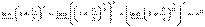
Дата добавления: 2015-09-10; просмотров: 87 | Поможем написать вашу работу | Нарушение авторских прав |