
Читайте также:
|
Теорема 4.2. Пусть функции  и
и 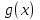 имеют в точке
имеют в точке  пределы и эти пределы соответственно равны
пределы и эти пределы соответственно равны  и
и  . Тогда функции
. Тогда функции  ,
,  имеют в точке
имеют в точке  пределы, равные соответственно
пределы, равные соответственно  Если кроме этого,
Если кроме этого,  , то в точке
, то в точке  существует предел функции
существует предел функции 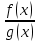 равный
равный  .
.
Доказательство. Пусть  - произвольная сходящаяся к
- произвольная сходящаяся к  последовательность значений аргумента, элементы которой отличны от
последовательность значений аргумента, элементы которой отличны от  . Тогда последовательности
. Тогда последовательности 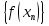 и
и 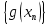 сходятся соответственно к пределам
сходятся соответственно к пределам  и
и  . Но тогда, в силу теоремы 3.7, последовательности
. Но тогда, в силу теоремы 3.7, последовательности
 и
и  (при
(при  ) имеют пределы, соответственно равные
) имеют пределы, соответственно равные 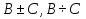 и
и  . Последнее утверждение, в силу определения предела функции по Гейне, означает, что
. Последнее утверждение, в силу определения предела функции по Гейне, означает, что  ,
,  ,
,  . Теорема 4.2 доказана.
. Теорема 4.2 доказана.
Теорема 4.3. Пусть функции 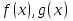 и
и 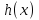 определены в некоторой окрестности точки
определены в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  и имеют в этой точке равные пределы. Пусть кроме этого выполняются неравенства
и имеют в этой точке равные пределы. Пусть кроме этого выполняются неравенства 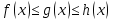 . Тогда существует
. Тогда существует  при этом
при этом 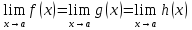 .
.
Доказательство. Пусть  - произвольная, сходящаяся к
- произвольная, сходящаяся к  последовательность, элементы которой отличны от
последовательность, элементы которой отличны от  . Тогда соответствующие последовательности
. Тогда соответствующие последовательности 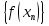 и
и  имеют предел, и эти пределы равны. Из условия теоремы следует, что
имеют предел, и эти пределы равны. Из условия теоремы следует, что  . Тогда согласно теореме 3.9
. Тогда согласно теореме 3.9  Следовательно, существует и
Следовательно, существует и  и при этом
и при этом 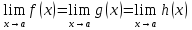 . Теорема 4.3 доказана.
. Теорема 4.3 доказана.
ВВЕДЕНИЕ
Определение предела. Число b – предел функции f(x) при x стремящемся к a, если для каждого положительного числа e можно указать такое положительной число d, что для всех x, отличных от a и удовлетворяющих неравенству | x-a |<d, имеет место неравенство |f(x)-b|<d.
Обозначение предела. Если b есть предел функции f(x) при x стремящемся к a, то записывают это так:
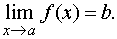
Определение непрерывной функции. Функция f(x) непрерывна в точке a, если

Вычисление пределов функций основано на применении следующих основных теорем:
ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть
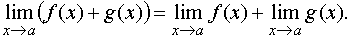
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть
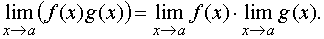
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть
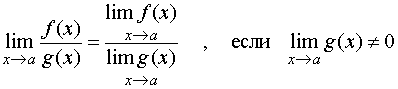
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля.
ТЕОРЕМА 4. Первый замечательный предел равен
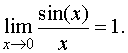
ТЕОРЕМА 5. Второй замечательный предел равен
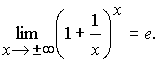
ТЕОРЕМА 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
перейти к содержанию
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ НА ОСНОВЕ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА
Пример 1. Докажем, что

Пусть задано произвольное e>0. Тогда для того чтобы выполнялось неравенство
| f(x)-a |<e, необходимо выполнение неравенства | x - a |<e, которое, очевидно, выполняется, если | x - a |<d, где d=e. Таким образом, согласно определению предела функции, число a, действительно, является пределом функции x при x стремящемся к a.
Пример 2. Докажем, что

Нужно доказать, что при произвольном e>0 найдется такое положительное d, что неравенство

будет выполняться, если |x-1|<d. Но, если x не равно 1, то (1) эквивалентно неравенству

или

При произвольном e неравенство (1) будет выполняться, если будет справедливо (2), а последнее справедливо, если |x-1|<d, где d=e. Поэтому в соответствии сопределением предела функции данная функция при x стремящемся к 1 имеет пределом число 2.
перейти к содержанию
ВЫЧИСЛЕНИЕ НЕСЛОЖНЫХ ПРЕДЕЛОВ
Дата добавления: 2015-09-10; просмотров: 198 | Поможем написать вашу работу | Нарушение авторских прав |