Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Производная обратной функции. Производная показательно-степенной функции.

I) Производная обратной функции:

Теорема:

(Пусть функция f(x) непрерывна и строго монотонна в окрестности точке x₀. Если существует производная обратной x=f(y) в точке y₀, то существует производная самой функции в точке x₀ и y^’_x=1/x^’_y).

Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функция y=f(x) дифференцируема, и y^’=1/g^’(y).

Доказательство:

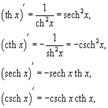Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом: Δx=g(y + Δy) − g(y). Тогда:

II) Производная показательно-степенной функции называется функция вида y[U(x)]^V(x).

1. Первый способ:

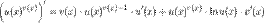
То есть вначале производная берется как от степенной функции, а потом как от показательной.

Замечание: Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:

2. Второй способ:

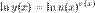
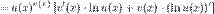
16. Производные основных функций: sin(x), cos(x), tg(x), ctg(x), lg(x), arcsin(x), arcos(x), arctg(x), arcctg(x), a^x, xⁿ и гиперболических функций.

ln ^’ x=1/x

(a^x) ^’ = (a^x)*ln a.

Производные гиперболических функций:

17. Производная функции заданной параметрически.

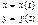Пусть x=x(t), y=y(t), тогда какому-то x, будет соответствовать какое-то значение t (t=f(x)), поэтому t будет соответствовать y и можно говорить, что y является функцией x (y=(x)), можно говорить, что y ^’_x. Заданная функция называется параметрически заданной функцией.

Теорема: Пусть y(x) задана параметрически уравнением (выше) предположим, что эти функции дифференцируемы и функция x=x(t) имеет обратную функцию t=f(x), тогда y ^’ _x, будет y ^’ _x=(y ^’ (t))/(x ^’ (t)). Из системы следует, что y=y(f(x)), y ^’ _x= y ^’ (t)*f ^’ (x) (По теореме производных обратной функции).