Читайте также:
|
Принцип Лагранжа известен также под названием начала варьирования деформированного состояния. О нем иногда говорят и как об энергетической трактовке метода перемещений.
3.1. Кинематически возможное варьирование. Возможные перемещения и деформации. Примем смещения за основные неизвестные и назовем кинематическим варьированием такой процесс изменения смещений, при котором остаются неизменными внешние нагрузки. Если к тому же сохраняют силу геометрические граничные условия (2.7), то такое варьирование смещений будем называть кинематически возможным.
Смещения, согласные с геометрическими связями (2.7), наложенными на тело, назовем возможными в отличии от истинных (или действительных) смещений, фактически реализуемых в теле за счет действия заданных внешних сил. Ясно, что истинные смещения удовлетворяют всем исходным данным и соотношениям теории упругости. Что касается возможных смещений, то от них требуется лишь согласие с геометрическими граничными условиями. Поэтому можно говорить о множестве возможных перемещений, всегда содержащем единственные истинные смещения.
Пусть 
— истинные смещения, а 
— близкие к ним возможные смещения. Очевидно, что
| (3.1) |
Смещениям отвечают истинные деформации
а смещениям — возможные деформации
Беря их разность, с учетом коммутативности операций варьирования и дифференцирования по пространственным координатам находим
| (3.2) |
Как видим, величины (3.2) вычисляются через вариации смещений по тем же соотношениям Коши, и поэтому их естественно назвать кинематически возможными вариациями деформаций.
3.2. Принцип Лагранжа. Хорошо известно, что тела, деформируемые обратимым образом, способны аккумулировать в себе потенциальную энергию 
, которая, если теперь воспользоваться терминологией вариационного исчисления, является функционалом, определенным на множестве функций-смещений, т.е.
| (3.3) |
Здесь интегрирование распространяется на весь объем тела, а подынтегральная функция
| (3.4) |
— удельная потенциальная энергия, являющаяся, как известно, однозначной функцией своих аргументов (
).
Внешние силы, действующие на упругое тело, совершают работу
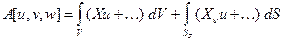
являющуюся линейным функционалом перемещений.
Назовем полной энергией тела функционал
Принцип Лагранжа гласит:
Дата добавления: 2015-09-10; просмотров: 146 | Поможем написать вашу работу | Нарушение авторских прав |