Читайте также:
|
В случае линейно упругого тела 
начало наименьшей работы выглядит следующим образом
и здесь, как видно, нет необходимости вводить понятие дополнительной потенциальной энергии, так как она фактически совпадает с обычной потенциальной энергией тела, выраженной через напряжения.
4.4. Теорема Кастильяно. Пусть 
— некоторое обобщенное смещение в теле, обусловленное действующими на него внешними силами. В качестве могут выступать смещение точки в фиксированном направлении, взаимное смещение двух точек, например, вдоль соединяющей их линии и т. п. Как подсчитать подобное смещение? Ответ на этот вопрос дает теорема Кастильяно.
Ради простоты рассуждений будем считать, что — искомое смещение некоторой внутренней или граничной точки тела в каком-то фиксированном направлении. Первое, что предстоит сделать, так это выяснить то, каким образом ввести интересующее нас смещение в функционал полной дополнительной энергии тела, из экстремальности которого мы намереваемся получить формулу для его вычисления. Единственную такую возможность предоставляет работа реактивных сил в связях, конечно, при условии, что в рассматриваемой точке имеется связь в направлении искомого смещения. Чаще всего ее может и не быть. Однако, ничто не мешает сначала ввести такую связь фиктивно, а затем в окончательных результатах ее убрать.
Итак, предположим, что в рассматриваемой точке тела в направлении искомого смещения имеется фиктивная связь, со стороны которой на тело действует сила 
, направленная так же, как и искомое смещение. Заметим, что эта связь необычная: она не противодействует, а способствует искомому перемещению. Не станем задумываться, как она устроена. Для наших рассуждений это не имеет никакого значения, ибо потом мы эту связь устраним.
Пусть нам как-то удалось найти напряженное состояние, вызванное совместным действием заданных сил и силы . Для тела с фиктивной связью это состояние истинное. Погрузим его в класс напряженных состояний, порождаемых лишь малыми изменениями 
силы , обусловленными, скажем, какой-то перенастройкой фиктивной связи (детали этого процесса несущественны). Заметим, что новые напряженные состояния статически возможны: изменения силы (реакции фиктивной связи) не нарушают уравнений (4.1), (4.2).
Условие стационарности полной дополнительной энергии тела с фиктивной связью запишется теперь так
Здесь 
— первая вариация полной дополнительной энергии самого тела (без фиктивной связи, но с учетом действия ее реакции), обусловленная малым изменением силы . Эта энергия — функция только фиктивной силы : 
. Чтобы подчеркнуть это, мы пометили ее сверху тильдой. Следовательно,
Величина 
, в отличие от интересующего нас смещения , обусловлена еще и действием силы : 
при 
. Учитывая, что 
, из двух последних равенств находим
В этом и состоит теорема Кастильяно, которую уже для общего случая можно сформулировать так:
Для того чтобы найти некоторое обобщенное смещение точки или системы точек тела, необходимо подобрать и приложить дополнительно к телу соответствующую этому смещению обобщенную силу, подсчитать полную дополнительную энергию тела и найти значение ее производной по обобщенной силе при нулевом значении последней.
Направление перемещения определяется знаком результата: положительный знак говорит о том, что смещение происходит в направлении выбранной обобщенной силы. Ради этого правила была введена столь необычная фиктивная связь.
В тех случаях, когда роль обобщенной силы может играть одна из заданных внешних сил, обозначим ее тем же символом ,
В условиях начала наименьшей работы имеем соответственно
Наконец, следует иметь в виду, что в случае линейно упругого тела 
, .
4.5. Пример. Для балки, показанной на рис. 4.1, найти прогиб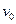 
и угол поворота 
свободного конца.
Заданная сила 
вызывает в балке изгибающий момент 
. Ее можно принять за обобщенную силу, отвечающую прогибу 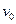. Поскольку 
и
то согласно теореме Кастильяно
Обобщенная сила для угла — момент на конце балки. Тогда
Так как 
, а 
, то свободный конец смещается по направлению силы , а сечение на свободном конце поворачивается в направлении, противоположном указанному моментом .
Дата добавления: 2015-09-10; просмотров: 100 | Поможем написать вашу работу | Нарушение авторских прав |