,
называемому основным вариационным уравнением Лагранжа.
Принимая во внимание тождества
после преобразований с помощью формулы Остроградского-Гаусса
(
— направляющие косинусы внешней единичной нормали поверхности 
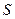) приходим к равенству
из которого вытекают статические соотношения (2.3), (2.4).
Таким образом, принцип Лагранжа эквивалентен статическим уравнениям теории упругости и может использоваться вместо них.
3.3. Применение принципа Лагранжа к теории изгиба балок. В этом пункте мы воспользуемся принципом Лагранжа с целью вывода дифференциального уравнения упругой линии балки и балочных статических граничных условий. Напомним с этой целью известные положения из теории изгиба балок.
Пусть балка длиной l находится в состоянии равновесия под действием распределенной поперечной нагрузки 
и сосредоточенных поперечных сил 
, 
и моментов 
, 
, приложенных соответственно на левом (
) и правом (
) концах балки; 
— координата вдоль оси балки (см. рис. 3.1).
 |
— жесткость балки на изгиб, зависящую, вообще говоря, от , а через 
, 
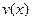и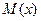 
— соответственно прогиб балки, перерезывающую силу и изгибающий момент. Три последние величины связаны между собой известными соотношениями
| (3.7) |
Уравнение упругой линии балки имеет вид
(3.8)
а балочные статические граничные условия – вид
| (3.9) |
или в смещениях
| (3.10) |
Выведем уравнение (3.8) и соотношения (3.10) из принципа Лагранжа.
Функционал полной энергии балки имеет вид
Для потенциальной энергии изгиба балки имеет место выражение
,
а для работы внешних сил — формула
.
Поэтому
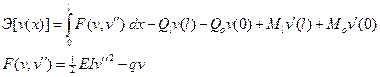
Полученное выражение полной энергии балки напоминает функционал (1.21). Поэтому согласно (1.23)
Приравнивая это выражение нулю, найдем
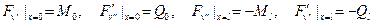
Замечая, далее, что
имеем
что в точности совпадает с (3.8) и (3.10).
В заключении заметим, что все выводы настоящего пункта и другие результаты, подобные им, справедливы при более слабом требовании — выполнении принципа стационарности полной энергии тела. Это требование составляет лишь необходимую часть утверждения принципа Лагранжа.
Дата добавления: 2015-09-10; просмотров: 92 | Поможем написать вашу работу | Нарушение авторских прав |