Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Разложение элементарных функций в ряд Маклорена

1. .

Согласно теореме о необходимом и достаточном условии сходимости ряда Тейлора к функции 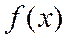полученный ряд сходится к функции и можно написать равенство:

. (1*)

Найдем интервал сходимости этого ряда. По общему признаку Д’Аламбера

Þ

ряд Маклорена сходится на всей числовой оси, т.е. для всех .

Заменим х на (- х):

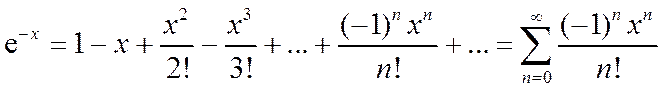
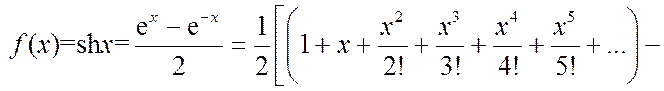
2.

(2*)

(нечетные степени с факториалами, все с плюсами)

3. (3*)

(четные степени с факториалами, все с плюсами). Разложение (3*) можно также получить с помощью почленного дифференцирования ряда (2*).

4. Найдём сумму бесконечно убывающей геометрической прогрессии со знаменателем , :

.

Переписав это равенство справа налево, получим разложение в ряд функции :

(4*)

5. В разложении (4*) выполним замену х на (- х). Тогда :

(5*)

6. Проинтегрируем ряд (5*) почленно от 0 до переменного предела х:

.

Получили разложение натурального логарифма:

(6*)

(без факториалов). Интервал сходимости по теореме об интегрировании степенных рядов остался прежним. Исследуем сходимость ряда на концах интервала. При получим знакопеременный гармонический ряд 7°, сходящийся по теореме Лейбница:

.

При получаем и расходящийся гармонический ряд. Таким образом, интервал сходимости ряда (6*) .

7. В разложении (5*) заменим х на (х ²):

Проинтегрируем почленно этот ряд:

. (7*)

(нечетные степени без факториалов). При получим сходящийся по Лейбницу ряд (8°):

.

При - тот же ряд, но с противоположными знаками:

.

Таким образом, интервал сходимости ряда (7*) .

8.

, ,

, ,

, ,

, ,

……………………………………………………….

, .

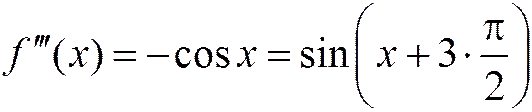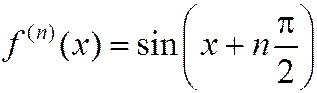Взятие производной – это поворот на 90° (нрис.2.10.3). Производные любого порядка ограничены: на : . Поэтому по теореме 2 , и функция разлагается в сходящийся к ней на ряд Маклорена по степеням x:

(8*)

Покажем, что полученный ряд сходится на всей числовой оси. По общему признаку Д’Аламбера:

сходится при всех х.

Ряд (8*) отличается от разложения гиперболического синуса (2*) знакопеременностью.

9. .

Почленным дифференцированием ряда (8*) получаем разложение косинуса в ряд Маклорена:

Таким образом,

(9*)

Т.к. ряд (9*) получен путем дифференцирования ряда (8*), то по теореме о дифференцировании степенных рядов ряд (9*) имеет тот же интервал сходимости, что и ряд (8*).

Ряд (9*) отличается от разложения гиперболического косинуса (3*) знакопеременностью.