Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Создание метода вариаций

Существенным недостатком метода Эйлера была его громоздкость. Уже в случае простейшей задачи на экстремум интеграла

для получения соответствующего дифференциального уравнения Эйлеру приходится проводить трудные вычисления. Выводы значительно усложняются, если перейти к более общим вариационным задачам.

Эйлер не рассматривал в своей книге пространственной задачи на экстремум интеграла

и задач на экстремумы кратных интегралов. А именно такие сложные задачи возникали в практике, и прежде всего в механике. При распространении на эти задачи своего метода, весьма громоздкого уже в простейшем случае, Эйлер встречал значительные трудности. Необходимо было усовершенствовать математический аппарат. Эйлер хорошо понимал это. Так, решая пространственную задачу о движении жидкости, он пишет, что созданный им «метод достаточно разработан только для фигур на плоскости». Эйлер продолжал искать новые методы решения вариационных задач. Он стремился решить вариационные задачи, используя аналогию с дифференциальным исчислением. Эйлер понимал, что речь идет об объектах более общей природы, о функциях, зависящих от линии (по современной терминологии, о функционалах).

И вот на эти более общие функции Эйлер хочет распространить основной принцип, с помощью которого строится теория экстремума функций конечного числа переменных: в точке экстремума производная равна нулю. В «Методе нахождения» Эйлер ищет метод, который позволил бы к решению вариационных задач непосредственно применить аппарат дифференциального исчисления. При этом Эйлер пришел к необходимости доказать некоторое соотношение, послужившее исходным пунктом в исследованиях Лагранжа:

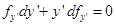(1)

или в обозначениях Эйлера

Лагранж доказал соотношение (1), применяя интегрирование по частям, и таким образом получил недостающее звено в рассуждениях Эйлера, посвященных созданию нового вариационного метода. Изучение работ Эйлера и Лагранжа и их переписки делает совершенно очевидной тесную связь работ Лагранжа по созданию метода вариаций с исследованиями Эйлера.

Первой работой Лагранжа по вариационному исчислению был «Опыт нового метода для определения максимумов и минимумов неопределенных интегральных формул». Во вводной части Лагранж, отправляясь от «Метода нахождения» Эйлера, отмечает те главы книги, которые Эйлер посвятил поискам нового метода. Непосредственно за этим Лагранж в нескольких предложениях излагает основы метода вариаций. Для решения задачи об экстремуме интеграла Лагранж предлагает по аналогии с теорией экстремума в дифференциальном исчислении найти производную рассматриваемого выражения и приравнять ее к нулю.

Исследования Лагранжа по вариационному исчислению тесным образом связаны с его работой в области механики. Одновременно с первым мемуаром, излагающим метод вариаций, Лагранж опубликовал статью «Приложение метода, изложенного в предыдущем мемуаре, для решения различных задач динамики».

Исчисление вариаций позволило Лагранжу решить новые классы задач механики. В первой же задаче, которую он рассматривает в статье, требуется найти движение тела, притягиваемого к произвольному числу неподвижных центров силами, являющимися функциями расстояний. Принцип наименьшего действия приводит к задаче отыскания экстремума интеграла вида

в классе пространственных кривых , , метод решения которой до Лагранжа был неизвестен.

В 1788 г. выходит в свет «Аналитическая механика» Лагранжа, открывшая новый этап в развитии механики. В этом произведении, написанном через сто лет после «Начал» Ньютона, вся мощь усовершенствованного математического аппарата была использована для построения механики. Результаты Эйлера, Даламбера и других ученых XVIII в. здесь обработаны и развиты с единой точки зрения. Основная для Лагранжа идея построения механики как систематического и гармоничного здания, возводимого на фундаменте единой общей предпосылки, пронизывает «Аналитическую механику».

Лагранж подчеркнул, что в основе решения задач механики лежит соединение принципа наименьшего действия с методом вариаций.

Таким образом, с Лагранжа началась новая эпоха в развитии вариационного исчисления. Используя метод вариаций, Лагранж значительно усовершенствовал аппарат аналитической механики. Это были открытия большого значения. Однако вначале они встретили холодный прием, так как исчисление вариаций не было понято современниками Лагранжа, и вскоре после выхода в свет его первого мемуара появились неодобрительные отзывы о методе Лагранжа, попытки заменить его или усовершенствовать. Этот холодный прием становится понятным, если учесть, что Лагранж ни при опубликовании своего метода, ни позже не выяснил его сущности, он только утверждал, что его метод основан исключительно на дифференцировании. Естественно, возникали сомнения в возможности применения дифференцирования к новому кругу задач.

Эйлер разъяснил исчисление вариаций, разработал его и ввел в широкую практику. Его работы «Элементы исчисления вариаций» и «Аналитическое изложение метода максимумов и минимумов» сыграли большую роль в развитии нового метода. В них Эйлер назвал новый алгоритм методом вариаций, а математическую дисциплину, изучающую экстремумы интегралов,— вариационным исчислением.

Идеи первого периода творчества Эйлера были надолго забыты. Однако они имеют не только исторический интерес. В конце XIX в. и XX в. прямой метод Эйлера, идея которого состоит в трактовке вариационной задачи как предельной для некоторой задачи на экстремум функции многих переменных, приобрел основное значение. Наряду с конечно-разностным приемом Эйлера развитие получили и другие прямые методы. Эти методы успешно применяются в тех вариационных задачах, для которых уравнение Эйлера не интегрируется в конечном виде, а также для решения самих дифференциальных уравнений, которые удается представить как уравнение Эйлера для некоторой вариационной задачи.

Эйлер сделал ясным понятие вариации. Он указал, что в вариационном исчислении искомая кривая сравнивается с бесконечно близкой к ней кривой, причем , не что иное, как бесконечно малые приращения величин , , получающиеся при переходе от искомой кривой к соседней, т. е. — приращение ординаты, — приращение производной. Выяснилось, что в методе вариаций изучается разность между значениями интегралов, взятых вдоль искомой кривой и соседней с ней кривой

(2)

Очевидно, что эта разность должна быть положительна в случае, когда на кривой интеграл принимает минимальное значение, отрицательна — когда интеграл принимает максимальное значение. Разность (2) разлагается по формуле Тейлора

, (3)

причем величины первого порядка малости относительно , составляют первую вариацию интеграла , имеющую вид

Для того чтобы на некоторой кривой интеграл принимал экстремальное значение, необходимо, чтобы на этой кривой первая вариация обращалась в нуль:

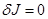или .

Так было получено исходное для рассуждений Лагранжа соотношение , которое он получал простым дифференцированием. Таким образом, Эйлер выяснил сущность метода вариаций. Новое исчисление перестало выглядеть как таинственное дифференцирование, которое неизвестно почему дает правильные результаты для вариационных задач.

Изучение разности (3) с точностью до бесконечно малых второго порядка дало основу для создания теории второй вариации и привело к отысканию достаточных условий экстремума интегралов. Рассмотрение второй вариации явилось новым этапом в развитии вариационного исчисления.