Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Рассмотрим способ получения эллиптически поляризованного излучения.

Допустим, что из двоякопреломляющего кристалла вырезана пластинка таким образом, что оптическая ось лежит в плоскости среза. Допустим далее, что излучение падает на пластинку перпендикулярно плоскости среза (рис.3). В этом случае колебания электрического вектора как в обыкновенной волне (), так и в необыкновенной (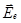) совершаются согласованно (когерентно).

Необходимо заметить также, что направления электрических векторов обыкновенного и необыкновенного лучей взаимно - перпендикулярны, в то время как волновые фронты параллельны друг другу (плоскости: АА¢ – для обыкновенного луча и ВВ¢ – для необыкновенного луча). Видно, что обыкновенная и необыкновенная волны распространяются в одном направлении, но с разными скоростями. В связи с этим между ними возникает разность хода:

Δ L = (n _o - n _e) d, (7)

где d – расстояние, проходимое обеими волнами в кристалле,. n _o и n _e показатели преломления обыкновенного и необыкновенного лучей.

При наличии разности хода волны могут интерферировать только в том случае, если они когерентны. Если падающее на кристалл излучение не поляризовано, о - и е - волны испускаются разными группами атомов (не согласованно), поэтому когерентности нет. Если же на кристалл падает линейно поляризованный свет, то волна, излучённая каждым атомом, разделяется между о - и е - волнами в пропорции, которая зависит от ориентации плоскости колебаний. Поэтому возникающие о - и е - компоненты когерентны и способны интерферировать.

Из теории сложения колебаний известно, что, при сложении взаимно перпендикулярных колебаний одинаковой частоты, конец результирующего вектора 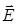движется по эллипсу (рис.4):

x²/ E_о² – (2 xy/ E_оE_е) cos δφ + y²/ E_е² = sin² δφ,

где δφ - сдвиг фаз колебаний, x и y - координаты конца результирующего вектора 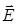: x º E_x, y º E_y. Нас интересует случай, когда эллипс ориентирован своими полуосями по осям Оx и Оy (Оу лежит в главной плоскости кристалла), при этом E_o и E_e являются полуосями эллипса. Это наблюдается, если выполнено условие для разности фаз: δφ = ± (π/2 + 2πk), k =0, 1, 2,... Уравнение эллипса преобразуется при этом к виду:

E_x²/ E_о² + E_y²/ E_e² = 1.

Разность фаз колебаний связана с разностью хода лучей: δφ = (2π/ λ₀)Δ L.. Используя (7), получаем:

d (n_o - n_e) = ± (λ₀ / 4 + k λ). (8)

Здесь "+" соответствует отрицательным кристаллам (n_o > n_e), "-" – положительным кристаллам (n_o < n_e). Таким образом, если толщина пластины, вырезанной вдоль оптической оси, удовлетворяет (8), результатом будет эллиптическая поляризация выходящего излучения. Такая пластина носит название четвертьволновой или пластины λ/4.

Как добиться циркулярной поляризации излучения? Эллипс превращается в окружность при условии равенства полуосей, т.е. E_o = E_e º E. Этого достигают, ориентируя четвертьволновую пластину оптической осью под углом α = 45⁰ к плоскости колебаний падающего излучения. При этом компоненты результирующего вектора 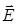удовлетворяют уравнению окружности: E_x² + E_y² = E².

Заметим, что в случаях: α = 0⁰ и α = 90⁰ из четвертьволновой пластины выходит плоско поляризованное излучение (электрический вектор представляет собой в первом случаеи во втором) с плоскостью колебаний, ориентированной как у падающего излучения.

Описание установки.

Излучение лазера 1 (рис. 5) проходит через поляризатор 2, анализатор 4 и попадает на фотодетектор 5. Фототок, пропорциональный интенсивности света, прошедшего через анализатор, измеряется микроамперметром 6, включённым в режиме измерения тока. В оптический канал может вводиться четвертьволновая пластина 3.

Рис. 5

Полупроводниковый лазер находится в цилиндрическом кожухе, укреплённом на стойке.

Поляризатор (2) размещается в полукруглом держателе на стойке. Анализатор (4) укреплён в поворотном элементе со шкалой для отсчёта угла в градусах и зубчатым колесом, облегчающим вращение. Четвертьволновая пластина смонтирована в круглой оправе с нанесённой по ободу шкалой по углу.

Переключатель режимов работы микроамперметра до начала и после окончания измерений должен находиться в положении " ¥ ". Для проведения измерений перевести переключатель в режим измерения постоянного тока, в котором получаются измеримые значения фототока (указываются в мкА).