Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Примеры решения задач. Задача 1. Выяснить определены ли на множествах N, Z, следующая операция:

Задача 1. Выяснить определены ли на множествах N, Z, 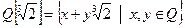следующая операция:

Решение. Согласно определения 1.1, бинарной алгебраической операцией на множестве А называется отображение прямого квадрата множества А в множество А, при котором любой упорядоченной паре элементов (a,b) соответствует единственный элемент с из А. Если операцию обозначить каким либо значком, например, ·, то это означает, что a · b = с Î А. Этим обозначением и будем пользоваться при решении задачи.

В этой задаче, согласно обозначениям, имеем a · b = а – b. Если a,b Î N, то а – b не всегда натуральное число, например, 2 – 5 = -3 Ï N, следовательно, вычитание не определено на N.

Если a,b Î Z, то а – b целое и, значит, вычитание есть бинарная алгебраическая операция на Z.

Пусть a,b Î = , т.е. а = , b = . Найдем a · b = а – b = () – () = (х₁ + х₂) + (y₁ + y₂) , т.к. х₁ – х₂, y₁ – y₂ Î Q, то a · b Î . Вычитание определено на множестве .

Задача 2. Составьте таблицу Кэли для операции нахождения НОК на множестве

А = {1, 2, 3, 4, 6, 12}. Является ли она алгебраической на этом множестве?

Решение. Таблица Кэли применяется для задания операции на конечном множестве. Эта таблица состоит из n строк и n столбцов, где на пересечении i -ой строки и j -ого столбца записывается результат операции . Составим таблицу Кэли для данной задачи.

a · b = НОК(a,b). Применим правило нахождения НОК для заполнения таблицы. Например, НОК (3, 12) = 12 и т.д. Из таблицы видно, все результаты операции нахождения НОК принадлежат множеству А. Следовательно, она является алгебраической на А.

Задача 3. Является ли коммутативной, ассоциативной операция на множестве R.

Решение. По определению коммутативности ·, надо показать, что " a,b Î R: а · b = b · а.

Найдем а · b и b · а: ; ; сравним результаты. a+b = b+a по свойству коммутативности на множестве R, значит , поэтому а · b = b · а.

Проверим ассоциативность ·, по определению ассоциативности " a,b,c Î А (а · b) · c = а · (b · c). Найдем результаты выполнения операции · левой и правой частей:

(а · b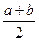) · c = · c = = ;

а · (b · c) = а · = = .

Следовательно, · не ассоциативна на R.

Задача 4. Найдите нейтральный элемент относительно операции умножения на множестве чисел 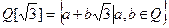. Укажите все симметризуемые элементы.

Решение. Находим нейтральный элемент относительно операции умножения, он называется единицей. Будем находить по определению, т.к. е Î 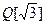, то е = , и он будет найден, если найдены х и y, причем х, y Î Q.

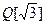Для любого из множества имеем равенство ()() = ()() = . Так как умножение коммутативно в 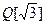, то достаточно рассмотреть

()() = Þ (ax + 3 by) + (ay +bx) = Þ

-----------------------------

(a² – 3 b²) y = ab - ba Þ y = 0 Þ bx=b Þ x =1

Значит, е = 1+0 = 1 – единица в .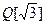

Симметричный элемент относительно умножения называется обратным. Найдем его по определению: 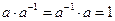. Обозначим . Тогда имеем: ()() = 1+0 . В результате получим систему аналогичную предыдущей:

Откуда имеем:

; , если

Надо, чтобы х, y Î Q, видим, что это так, если , т.е. если Þ 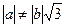, т.к. а Î Q, то это неравенство выполняется для любого рационального а.

Аналогично рассуждая, получаем, что неравенство выполняется для любого рационального числа b. Ясно, что 3 b² – a² = 0 при условии, что a=b= 0. Поэтому, делаем вывод, что для " ¹ 0 существует обратный элемент равный + .