Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Интерполяция таблиц смертности для дробных возрастов. Линейный подход.

X=k+u; k=[x]; u={x}; 0≤u≤1

S(x)=S(k+u)

l_x и S(x) линейны на [k;k+1]

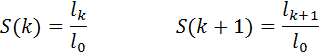
l_x=l_k+u= l_k+u(l_k+1- l_k)= l_k-u*d_k

S(x)=S(k+u)= S(k)+u*[ S(k+1)- S(k)]= S(k)*[1- u*q_k ]

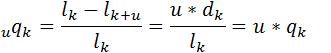
S’(k+u)= -S(k)*q_k => μ_k+u= q_k /(1-u*q_k)

_up_k=1-u*q_k

Интерполяция таблиц смертности для дробных возрастов. Условие постоянства силы смертности.

X=k+u; k=[x]; u={x}; 0≤u≤1

S(x)=S(k+u)

Условие постоянства силы смертности:

(μ_х= μ_k+u= μ_k)

=> имеем exp на [k;k+1]

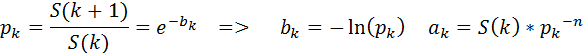
Интерполяция таблиц смертности для дробных возрастов. Условие Балдуччи.

X=k+u; k=[x]; u={x}; 0≤u≤1

S(x)=S(k+u)

Условие Балдуччи: 1/S(x) линейны на [k;k+1]

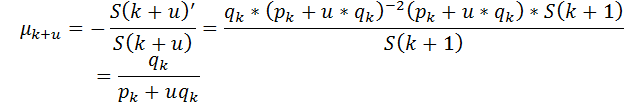
10. Средняя продолжительность жизни – полная и округленная, их связь.

Полная средняя продолжительность оставшейся жизни индивида в возрасте х – математическое ожидание Т_х.

Выражается через функцию дожития

Округленная продолжительность жизни в возрасте х.

Если учитывать, что S(x) линейна на [x+k;x+k+1], то получаем следующую связь:

e_x^o=e_x+1/2