
Читайте также:
|
1. Матрицы. Линейные операции над ними и их свойства.
Матрицей называется прямоугольная таблица чисел, содержащая m строк
одинаковой длины.

Матрицы равны между собой, если равны все их соответствующие элементы.
Матрица, у которой число строк и столбцов равно – называется квадратной.
Матрица, все элементы которой, кроме элементов главной диагонали равны нулю,
называется диагональной.
Диагональная матрица, у которой все элементы главной диагонали равны 1,
называется единичной. Обозначается буквой Е.
Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю,
называется треугольной.
Матрица, у которой все элементы равны нулю, называется нулевой.
1. 
2. 
3. 
4. 
5. 
6. 
7. 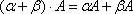
8. 
2. Умножение матриц. Транспонирование. Свойства.
Операция умножения возможна, если количество столбцов первой матрицы равно
количеству строк другой матрицы.

где 

1. 
2. 
3. 
4. 
Матрица, полученная заменой каждой ее строки столбцом с тем же номером,
называется матрицей транспонированной, к данной.
1. 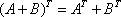
2. 
Дата добавления: 2015-01-30; просмотров: 100 | Поможем написать вашу работу | Нарушение авторских прав |