Читайте также:
|
В силу изменчивости условии измерений никакое измерение не может быть выполнено абсолютно точно. Его результат всегда содержит некоторую ошибку, т.е. мы всегда получаем нужную величину с некоторой погрешностью. Поэтому в задачу измерений входит не только нахождение самой величины, но также и оценка допущенной при измерении погрешности.
Все погрешности измерений делятся на 3 класса: систематические, случайные, промахи.
Случайная составляющая погрешности измерения также не может быть исключена полностью, но её влияние можно уменьшить рациональной обработкой результатов измерения.
Отдельный результат измерения, т.е. отдельное значение случайной величины, предсказать невозможно. Большая же совокупность результатов измерения и случайных погрешностей подчиняется определенным закономерностям, которые могут быть учтены при обработке результатов измерений с использованием методов математической статистики и теории вероятностей.
Наиболее общей характеристикой случайной величины является плотность распределения вероятностей
(1.2)
где 
- вероятность значений случайной величины х в интервале dx.
Полностью свойства случайной величины описываются функцией распределения F(х), которая определяет вероятность того, что случайная величина х будет меньше хi:
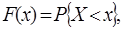(1.3)
Функция распределения является неубывающей функцией и определяется в интервалах F(- 
) = 0, a F(+ ) = 1.
Рисунок 1 Пример построения функции распределения случайных величин F(х).
Аналитическим выражением нормального закона распределения ошибок является формула Гаусса
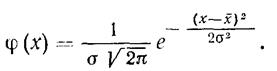
Если измеряемая величина является суммой двух и более величин, то суммарная дисперсия или средние арифметические ошибки определяются по формулам
,
.
Дата добавления: 2015-01-30; просмотров: 98 | Поможем написать вашу работу | Нарушение авторских прав |