Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Точечные оценки истинного значения и среднеквадратического отклонения. Оценка с помощью интервалов.

Для оценки точности результатов отдельных измерений и их среднего арифме­тического в статистической теории погрешностей вводятся следую­щие показатели точности:

- средние квадратические погрешности;

- вероятные погрешности;

- средние арифметические погрешности.

Значения этих погрешностей для ряда отдельных измерений, оп­ределяются по формулам:

; (1.10)

; (1.11)

,

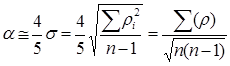где - средняя арифметическая погрешность ряда измерений;

- вероятная погрешность ряда измерений;

- средняя квадратичная погрешность ряда измерений;

- число измерений;

- остаточные погрешности.

Погрешности результата измерений (среднего арифметического) исчисляются по формулам:

, (1.12)

, (1.13)

, (1.14)

где Е – вероятная погрешность результата;

S – средняя квадратическая погрешность результата;

А – средняя арифметическая погрешность результата.

Из приведенных выражений следует, чем больше n, тем выше
точность. Однако это увеличение точности, начиная с ,
растет незначительно.

Практическое значение имеют понятия абсолютных и относительных погрешностей.

Абсолютная погрешность - погрешность в единицах измеряемой величины - должна всегда сопровождаться наименованием единиц.

Относительная погрешность - определяется как отношение чис­ленного значения абсолютной погрешности к численному значению результата измерений.

Например, если результат измерения представлен как , то соответствующее значение относительной погрешности равно: ,

где Мср - среднее арифметическое ряда измерений;

Е - абсолютная вероятная погрешность.

8. Проверка нормальности распределения результатов наблюдений. Обнаружение грубых погрешностей.

Границы неисключенной систематической погрешности θ результата измерения вычис­ляют путем построения композиции неисключенных систематических погрешностей средств изме­рений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле

,

где θ_i, — граница i -й неисключенной систематической погрешности:

k — коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности Р = 0,95.

При доверительной вероятности Р = 0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (т > 4). Если же число суммируемых погрешностей равно четырем или менее четырех (т < 4), то коэффициент k определяют по графику зависимости (см. чертеж).

График зависимости k =f(m, l)

0123^557 l

k=f(m,l), где т — число суммируемых погрешностей;

; кривая 1 - m=2; кривая 2 - m=3; кривая 3 - m=4.