Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Формула полной вероятности и формула Байеса

Если событие может наступить только при появлении одного из несовместных событий (гипотез) , то вероятность события вычисляется по формуле полной вероятности: , где - вероятность гипотезы 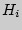, - условная вероятность события при выполнении гипотезы (.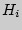

Проиллюстрируем формулу полной вероятности на графе с выделенной вершиной:

Полная вероятность события равна весу всего вероятностного графа с гипотезами.

С формулой полной вероятности тесно связана формула Байеса. Если до опыта вероятности гипотез были , ,..., , а в результате опыта появилось событие , то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса

Формула Байеса дает возможность "пересмотреть" вероятность гипотез с учетом наблюдавшегося результата опыта. Условная вероятность может находиться как отношение веса ветви, проходящей через вершину, соответствующую гипотезе , к весу всего вероятностного графа.

6. Случайные величины: дискретные и неприрывные. Закон распределения дискретной случайной величины

Случайная величина – это величина, значение которой зависит от случая, т.е. от элементарного события . Таким образом, случайная величина – это функция, определенная на пространстве элементарных событий . Примеры случайных величин: количество гербов, выпавших при независимом бросании двух монет; число, выпавшее на верхней грани игрального кубика; число дефектных единиц продукции среди проверенных.

Определение случайной величины Х как функции от элементарного события , т.е. функции , отображающей пространство элементарных событий в некоторое множество Н, казалось бы, содержит в себе противоречие. О чем идет речь – о величине или о функции? Дело в том, что наблюдается всегда лишь т.н. «реализация случайной величины», т.е. ее значение, соответствующее именно тому элементарному исходу опыта (элементарному событию), которое осуществилось в конкретной реальной ситуации. Т.е. наблюдается именно «величина». А функция от элементарного события – это теоретическое понятие, основа вероятностной модели реального явления или процесса.

Отметим, что элементы Н – это не обязательно числа. Ими могут быть и последовательности чисел (вектора), и функции, и математические объекты иной природы, в частности, нечисловой (упорядочения и другие бинарные отношения, множества, нечеткие множества и др.) [2]. Однако наиболее часто рассматриваются вероятностные модели, в которых элементы Н – числа, т.е. Н = R¹. В иных случаях обычно используют термины «случайный вектор», «случайное множество», «случайное упорядочение», «случайный элемент» и др.

Определение: Случайной называется величина, которая в результате испытания принимает только одно значение из возможного множества своих значение, наперед неизвестное и зависящее от случайных причин.

Различают два вида случайных величин: дискретные и непрерывные.

Определение: Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное.

Другими словами, возможные значения дискретной случайной величину можно перенумеровать.

Описать случайную величину можно с помощью ее закона распределения.

Определение: Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, в первой строке которой указаны в порядке возрастания все возможные значения случайной величины, а во второй строке соответствующие вероятности этих значений, т.е.

где р₁+ р₂+…+ р_n=1

Такая таблица называется рядом распределения дискретной случайной величины. Если множество возможных значений случайной величины бесконечно, то ряд р₁+ р₂+…+ р_n+… сходится и его сумма равна 1.

Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят ломаную, соединяющую последовательно точки с координатами (x_i;p_i), i=1,2,…n. Полученную линию называют многоугольником распределения (рис.1)

Закон распределения дискретной случайной величины Х может быть также задан аналитически (в виде формулы):

P(X=x_i)=φ(x_i),i =1,2,3…n