Читайте также:
|
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
23. Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.Переменными (неизвестными) транспортной задачи являются xij, i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю.Эти переменные могут быть записаны в виде матрицы перевозок. Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны
По условию задачи требуется обеспечить минимум суммарных затрат.Следовательно, целевая функция задачи имеет вид:
Система ограничений задачи состоит из двух групп уравнений.Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью.Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью.Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ северо-западного угла, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы. Рассмотрим простейший, так называемый способ северо-западного угла. Другой способ - способ минимальной стоимости по строке - основан на том, что мы распределяем продукцию от пункта Ai не в любой из пунктов Bj, а в тот, к которому стоимость перевозки минимальна. Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчетов и находим минимальную стоимость перевозки из оставшихся пунктов Bj. Во всем остальном этот метод схож с методом северо-западного угла. На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов.
Метод потенциалов позволяет, отправляясь от некоторого опорного плана перевозок, построить решение транспортной задачи за конечное число итераций (шагов). Общая схема отдельной итерации состоит в следующем. По данному опорному плану каждому пункту задачи сопоставляется число, называемое его предварительным потенциалом. Предварительные потенциалы выбираются так, чтобы их разность для любой пары пунктов,, связанных основной коммуникацией, была равна – стоимости перевозок между этими пунктами единицы продукта.
24. Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.Если ребра не имеют ориентации, граф называется неориентированным.
Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки
Простой граф граф без кратных ребер и петель.Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.
Граф отношения делимости-изображающий отношение делимости на множестве.Принцип такой: если от одного числа до другого есть цепь, ведущая вверх, тогда второе число делится на первое
Подграф графа это граф, являющийся подмоделью исходного графа, т.е. подграф содержит некоторые вершины исходного графа и некоторые ребра (только те, оба конца которых входят в подграф).
Подграф, порожденный множеством вершин U это подграф, множество вершин которого - U, содержащий те и только те ребра, оба конца которых входят в U.Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.
Граф называется связным, если любая пара его вершин связана.
Связными компонентами графа называются подграфы данного графа, вершины которых связаны.
Дерево — это связный граф без циклов.
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья. Граф без цикла называется лесом. Вершины степени 1 в дереве называются листьями.
25. Таким образом, теоретико-графовый подход позволяет изучать экономико-географические объекты с неизвестной метрикой пространства. Использование помеченных графов расширяет возможности количественного анализа явлений и процессов. Аппарат теории графов связан с теорией множеств, теорией отношений, матричной алгеброй, математическим программированием. К сожалению, он недостаточно используется в решении ряда проблем экономической географии: при районировании, исследовании территориально-производственных комплексов и промышленных узлов, при планировании различных линий (электропередач, нефте- и газопроводов, каналов связей и др.) производственной инфраструктуры.
Так как транспортная сеть - это сложная система, в функции которой помимо функций передачи входят также функции контроля, обслуживания и управления, то для ее описания используют функциональные модели. Транспортная модель сети основана на концепциях иерархического представления сети в виде слоев и разделения сети каждого слоя на части (рис.
Концепция иерархического представления транспортной сети в виде слоев основана на следующем:
Сеть каждого слоя содержит аналогичные функции.
Каждый сетевой слой может представлять отдельную сеть.
Модель сети в виде слоев позволяет определить управляемые объекты для создания сети управления (TMN).
Сеть каждого слоя может иметь собственные операционные процедуры обслуживания, такие как переключение на защиту, автоматическое восстановление после сбоев или отказов и другие.
Возможно добавление или замена слоя без воздействия на другие слои в отношении архитектуры.
Каждый слой сети может быть определен независимо от других слоев.
В каждом слое можно выделить три элементарные функции. На рис. 2.2 приведены графические обозначения этих функций (соединение, завершение, адаптация). Функции соединения обеспечивают возможность маршрутизации, защиты. К функциям завершения относится создание и чтение заголовков трактов, секций. К функциям адаптации могут относиться: скремблирование/дескремблирование,кодирование/декодирование, цифровая коррекция с управляемыми вставками и по прямой линии, сглаживание фазовых дрожаний, мультиплексирование/демультиплексирование, восстановление синхронизации, идентификация полезной нагрузки и т.д.
26. Если условия транспортной задачи заданы в виде картосхемы, на которой условно изображены поставщики, потребители и связывающие их дороги, указаны величины запасов груза и потребностей в нем, а также числа cijявляющиеся показателями принятого в задаче критерия оптимальности,то говорят, что транспортная задача поставлена в сетевой форме.
Описанную картосхему будем называть транспортной сетью. Пункты расположения поставщиков и потребителей будем изображать кружками и называть вершинами (узлами) сети, запасы груза будем записывать в кружках положительными, а потребности - отрицательными числами. Дороги, связывающие пункты расположения и потребления груза и другие пункты, будем изображать линиями и называть ребрами (дугами, звеньями) сети. При изображении транспортной сети реальный масштаб не соблюдается. На сети могут быть изображены вершины, в которых нет ни поставщиков, ни потребителей. Наличие таких вершин не повлияет на способ решения, если считать, что запасы (потребности) груза в них равны нулю. Такие вершины называют нулевыми (см. вершину II на рис. 2). Различия между транспортными задачами в матричной и сетевой формах весьма незначительны, так как методы их решения основаны на одних и тех же идеях. Далее мы будем использовать уже известный метод потенциалов.
Решение задачи на сети начинается с построения начального опорного плана. Поставки груза из вершины в вершину будем обозначать стрелками с указанием величин поставок.
Решение задачи на сети начинается с построения начального опорного плана.
Опорный план должен удовлетворять следующим требованиям:
1) все запасы должны быть распределены, а потребности удовлетворены;
2) к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;
3) общее количество стрелок должно быть на единицу меньше числа вершин;
4) стрелки не должны образовывать замкнутый контур
Далее следует проверить план на оптимальность.Для этого вычисляют потенциалы. Одной из вершин (например, вершине I) присвоим некоторое значение потенциала (например, равное 0). (Для большей наглядности потенциалы заключают в рамки.) После этого, двигаясь по стрелкам, определяют потенциалы остальных вершин, руководствуясь правилом: если стрелка выходит из вершины, то к потенциалу этой вершины прибавляем показатель Cij критерия оптимальности, если же направление стрелки противоположно, то Cij вычитаем.
После вычисления потенциалов находят характеристики ребер без стрелок по правилу: из большего потенциала вычитается меньший, а разность вычитается из показателя Cij, отвечающего данному ребру; если все ребра без стрелок имеют неотрицательные характеристики, то составленный план является оптимальным. Вырождение плана транспортной задачи в сетевой постановке внешне проявляется в том, что при полном использовании запасов и полном удовлетворении потребностей количество стрелок оказывается меньше, чем n - 1, где n - общее число вершин (включая и нулевые!).Способ преодоления вырождения весьма прост: дополнительно вводится нужное количество стрелок с нулевыми поставками. Направления стрелок выбираются произвольно, однако они не должны образовывать замкнутый контур.В случае открытой модели вводят фиктивного потребителя (поставщика) со спросом, равным небалансу. Фиктивный потребитель (поставщик) соединяется ребрами непосредственно со всеми поставщиками (потребителями). При этом показатели Cij ребер, соединяющих фиктивного потребителя (поставщика) с поставщиками (потребителями), следует брать одинаковыми и сравнительно большими. Делается это для того, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта.
27.Сетью называется граф, элементам которого поставлены в соответствие некоторые параметры. Далее элементы множества R будем называть узлами, а множества А – дугами.
Пусть каждой дуге 
некоторой сети 
поставлено в соответствие неотрицательное (действительное) число 
называемое пропускной способностью дуги.
Функция С, отображающая множество А в множество неотрицательных чисел, называется функцией пропускной способности. Пусть s и t – два различных узла из R. Стационарный поток величины v из s в t в сети 
есть функция f, отображающая множество А в множество неотрицательных чисел, удовлетворяющая линейным уравнениям и неравенствам
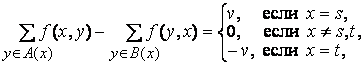
Где 
(«после x»), 
(«перед х»).
Будем называть узел s – источником, узел t – стоком, а остальные узлы – промежуточными.
Потоком в сети 
назовем функцию f, сопоставляющую каждому ребру сети целое число и обладающую следующими свойствами: 
(кососимметрия), 
(допустимость).
Дата добавления: 2015-01-30; просмотров: 102 | Поможем написать вашу работу | Нарушение авторских прав |