Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Математическое ожидание случайного вектора

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.

Свойства:

Дисперсия любой случайной величины неотрицательна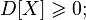

-Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

-Если случайная величина равна константе, то её дисперсия равна нулю: Верно и обратное: если то 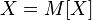почти всюду;

-Дисперсия суммы двух случайных величин равна:

где — их ковариация;

-Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

-В частности, для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

-

-

-

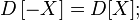
8 (Биномиальное, нормальное, равномерное распределение. Распределе­ние Пуассона.)

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p.

Функция распределения биномиального распределения может быть записана в виде суммы:

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности распределения:

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Значение: Важное значение нормального распределения во многих областях науки, например, в математической статистике и статистической физике вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования. Непреры́вное равноме́рное распределе́ние — в теории вероятностей - распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна.

Функция распределения

Так как плотность равномерного распределения разрывна в граничных точках отрезка, то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в теории массового обслуживания.