Читайте также:
|
, где 
- длина перпендикуляра, опущенного из начала координат на плоскость, а углы 
, 
и 
- углы, образованные этим перпендикуляром с осям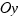и 
, 
и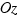 
соответственно.
19) Прямая в пространстве: общие уравнения, каноническое и параметрическое уравнения.
Рассмотрим прямую на плоскости. Общим уравнением прямой на плоскости называют уравнение 
. Если прямая задана в ортонормированном базисе и вектор 
имеет единичную длину, эта формула называется нормальным уравнением прямой.
Параметрическим уравнением прямой называют задание прямой в виде
Вектор (α,β) называют направляющим, а точку 
- начальной.
Каноническим уравнением прямой называют уравнение
Термины направляющий вектор и начальная точка вводятся для канонического уравнения так же, как и для параметрического уравнения (и имеют тот же смысл).
Каноническое уравнение прямой в пространстве Каноническое уравнение прямой в пространстве имеет вид:
Где, 
, 
, 
- координаты точки, лежаей на плоскости, а m, n и p - координаты направляющего вектора прямой.
Параметрическое уравнение прямой в пространстве Параметрическое уравнение прямой в пространстве имеет следующий вид: 
Дата добавления: 2015-01-30; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |