Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Свойства определителей

1. Общий множитель любой строки (столбца) можно выносить за знак определителя.
2. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.
3. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.
4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
5. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

4) Вычисление определителей п-го порядка: разложение определителя по строке, метод приведения к треугольному виду.

Квадратной м-це А порядка n можно сопоставить число дельта А(|А|, ∆), которое называется определителем, если:

– n=1, A=(a1), ∆A=a1;

– n=2, A=, ∆= =a11a22-a12a21;

–n=3, A=; ∆A=

Свойства определителей:

1. Если у определителя какая-л строка (столбец) состоит только из нулей, то ∆=0;

2. Если какие-л две строки (столбца) определителя пропорциональны, то ∆=0;

3. Если какую-л строку (столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число;

4. Если две строки (столбца) определителя поменять местами, то определитель изменит знак;

5. Если к какой-л строке (столбцу) определителя прибавить какую-л другую строку (столбец), умноженное на произвольное число, то определитель не изменится;

6. Определитель произведения матриц равен произведению их определителей.

5) Ранг матрицы. Вычисление ранга: метод окаймляющих миноров, метод элементарных преобразований.

Минором R-го порядка произвольной м-цы А называется определитель, составленный из элементов м-цы, расположенных на пересечении каких-либо R-строк и R-столбцов.

Рангом м-цы А называется наибольший из порядков ее миноров, неравных 0.

Базисным минором называется любое из миноров м-цы А, порядок которого равен рангу А.

При элементарных преобразованиях ранг м-цы не изменяется.

Ранг ступенчатой м-цы равен количеству ее не нулевых строк.

Свойства:

– при транспонировании м-цы ее ранг не меняется;

– если вычеркнуть из м-цы нулевой ряд, то ранг не изменится.

Метод элементарных преобразований.Этот метод основан на последней теореме из ☞ ПУНКТА: элементарные преобразования системы строк матрицы не изменяют ее ранга. Поэтому имеет смысл преобразовать исходную систему к такому виду, для которого величина ранга будет очевидна.

1. Ищем ненулевой элемент матрицы (если такого нет, то );
2. перестановкой строк и столбцов матрицы, добиваемся, чтобы ненулевой элемент попал в левый верхний угол;
3. применяя метод исключения Гаусса, добиваемся, чтобы все элементы первого столбца полученной матрицы, кроме верхнего, обратились в нуль;

4. к полученной в результате исключения подматрице порядка применяем процедуры пунктов 1-3.Процесс заканчивается, когда матрица оказывается приведенной к виду:

Тогда (числу оставшихся ненулевых строк).

Метод окаймляющих миноров.Очевидно, что если все миноры порядка 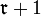для матрицы равны нулю, то и все миноры бóльшего порядка должны быть равны нулю. Но, оказывается, для проверки условия нет необходимости вычислять и все миноры порядка .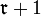

Для произвольного минора матрицы порядка

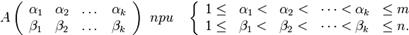
его окаймляющим минором называется минор 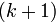-го порядка, получающийся приписыванием еще одной строки и одного столбца:

6) Обратная матрица. Вычисление обратной матрицы: с помощью присоединенной, методом элементарных преобразований.

Матрица А^-1 называется обратной к матрице А, если выполняется условие А* А^-1 = А^-1*А = Е

Всякая невырожденная матрица (т.е. ∆≠0) имеет обратную.

Алгоритм вычисления обратной матрицы:

1. вычисляем определитель, составленный по данной матрице;

2. находим матрицу А^Т, транспонированную к А;

3.

4. вычисляем обратную матрицу по формуле А^-1 = А^*/∆А = 1/∆А* ()

В данном контексте под элементарными преобразованиями понимается:

1. Умножение строки на любое ненулевое число.

2. Прибавление к одной строке любой другой, предварительно умноженной на любое число.

Алгоритм метода чрезвычайно прост по своей сути.

Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E:

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B). С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы):

TA = E Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A:

T = A ^-1.

Тогда TE = A ^-1 и, следовательно,

7)Система линейных уравнений: матричная форма, совместность, определенность. Теорема Кронекера-Капелли.

Система линейных уравнений может быть представлена в матричной форме как:

или:

A x = B.

Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.