Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Динамика вращательного движения абсолютно твердого тела. Момент силы. Работа при вращении абсолютно твердого тела вокруг неподвижной оси.

Пусть твердое тело вращается относительно оси под действием нескольких сил с суммарным моментом М относительно той же оси. Тогда работа этих сил приводит к изменению кинетической энергии этого тела.

, ,,

, ,

, ,

,

,

,

- основное уравнение динамики вращательного движения.

Момент силы относительно оси -проекция на эту ось вектора момента силы относительно любой точки, выбранной на данной оси.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*).

Полная работа

Если , то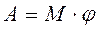

Кинетическая энергия абсолютно твнрдого тела, вращающегося вокруг относительно неподвижной оси. Момент инерции. Теорема Штейнера. Моменты инерции тел простейшей геометрической формы.

Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси.

Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m₁, m₂,…,m_n, находящиеся на расстоянии r₁, r₂,…, r_n, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусов r_i и имеют различные линейные скорости υ_i. Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов.

T_вр=∑ⁿ_i=1m_iυ_i²/2=∑ⁿ_i=1m_iω²r_i²/2=(ω²∑ⁿ_i=1m_ir_i²)/2=I_zω²/2, где I_z – момент инерции тела. Вращение твёрдого тела вокруг неподвижной оси:

Можно показать, что проекция момента импульса на ось “Z” может быть записана таким образом:

где R – расстояние до оси.

Момент инерции материальной точки относительно неподвижной оси - скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также , где - угловая скорость тела относительно данной оси.

Теорема Штейнера: Момент инерции твердого тела относительно некоторой оси вращения равен сумме момента инерции этого тела относительно оси параллельной данной и проходящей через центр масс тел и произведению массы тела не квадрат расстояния между осями.

· Обруч

· Цилиндр

· Круг

· Стержень, ось посередине

· Стержень, ось на конце