Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Ковариация, коэффициент корреляции.

Особую роль играет центральный момент порядка 1+1 или второй смешанный центральный момент, который называется ковариацией или корреляционным моментом m_1,1 (x, y) = K_{xy= (11.8)}

Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X и Y и характеризует степень линейной статистической зависимости величин X и Y и рассеивание относительно точки (m_x, m_y):

K_xy = ,

Свойства коэффициента корреляции:

1. Абсолютная величина коэффициента корреляции двух случайных величин не превышает единицы: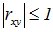

2. │r_xy│=1 если Y=aХ+b

27 билет

Свойства дисперсии

Свойства дисперсии следуют из соответствующих свойств математического ожидания. Заметим, что из существования второго момента следует существование математического ожидания случайной величины и конечность дисперсии.

Во всех свойствах ниже предполагается существование вторых моментов случайных величин.

D1.

Дисперсия может быть вычислена по формуле: .

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D[Х] = М[(Х – М[Х])²].

Билет