
Читайте также:
|
а. уравнение с угловым коэффициентом - 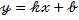
Число  = tg
= tg  называется угловым коэффициентом прямой, а уравнение
называется угловым коэффициентом прямой, а уравнение 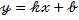 - уравнением прямой с угловым коэффициентом.
- уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то  и, следовательно, уравнение прямой будет иметь вид
и, следовательно, уравнение прямой будет иметь вид  .
.
Если прямая параллельна оси  , то
, то 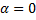 , следовательно,
, следовательно,  = tg
= tg  =0 и уравнение имеет вид
=0 и уравнение имеет вид  .
.
Если прямая параллельна оси  , то
, то  и уравнение теряет смысл, так как для нее угловой коэффициент
и уравнение теряет смысл, так как для нее угловой коэффициент  = tg
= tg  =tg
=tg  не существует. В этом случае уравнение прямой будет иметь вид
не существует. В этом случае уравнение прямой будет иметь вид  , где
, где  абсцисса точки пересечения прямой с осью
абсцисса точки пересечения прямой с осью  .
.
Доказательство: Пусть на плоскости  задана произвольная прямая, не параллельная оси
задана произвольная прямая, не параллельная оси  . Ее положение вполне определяется ординатой
. Ее положение вполне определяется ординатой  точки
точки 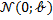 пересечения с осью
пересечения с осью  и углом
и углом  между осью
между осью  и прямой.
и прямой.
Под углом 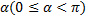 наклона прямой понимается наименьший угол, на который нужно повернуть вокруг точки пересечения прямой и оси
наклона прямой понимается наименьший угол, на который нужно повернуть вокруг точки пересечения прямой и оси  против часовой стрелки ось
против часовой стрелки ось  до ее совпадения с прямой.
до ее совпадения с прямой.
Возьмем на прямой произвольную точку  . Проведем через точку
. Проведем через точку  ось
ось  , параллельную оси
, параллельную оси  и одинаково с ней направленную. Угол между осью
и одинаково с ней направленную. Угол между осью  и прямой равен
и прямой равен  . В системе
. В системе  точка
точка  имеет координаты
имеет координаты  и
и  . Из определения тангенса угла следует равенство tg
. Из определения тангенса угла следует равенство tg  , т. е.
, т. е.  . Введем обозначение
. Введем обозначение  , получаем уравнение
, получаем уравнение 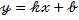 , которому удовлетворяют координаты любой точки
, которому удовлетворяют координаты любой точки  прямой.
прямой.
общее уравнение – 
Возможны два случая.
Если  , то уравнение имеет вид
, то уравнение имеет вид  , причем
, причем  , т. е.
, т. е.  . Это есть уравнение прямой, параллельной оси
. Это есть уравнение прямой, параллельной оси  и проходящей через точку
и проходящей через точку  .
.
Если  , то плу4чаем уравнение
, то плу4чаем уравнение 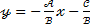 . Это есть уравнение прямой с угловым коэффициентом
. Это есть уравнение прямой с угловым коэффициентом  = tg
= tg  =
=  .
.
Есть частные случаи общего уравнение прямой:
1) Если  , то уравнение приводится к виду
, то уравнение приводится к виду  . Это есть уравнение прямой, параллельной оси
. Это есть уравнение прямой, параллельной оси  ;
;
2) Если  , то прямая параллельна оси
, то прямая параллельна оси  ;
;
3) Если  , то получаем
, то получаем  . Уравнению удовлетворяют координаты точки
. Уравнению удовлетворяют координаты точки  , прямая проходит через начало координат.
, прямая проходит через начало координат.
б. уравнение прямой, проходящей через две заданные точки –  (при
(при  ,
,  ).
).
Пусть прямая проходит через точки М1(x1;y1) и M2(x2;y2). Уравнение прямой, проходящей через точку М1, имеет вид y-y1=k(x-x1), где k- пока неизвестный коэффициент.
Так как прямая проходит через точку M2(x2;y2), то координаты этой точки должны удовлетворять уравнению y2-y1=k(x2-x1). Отсюда находим  . Подставляя найденное значение
. Подставляя найденное значение  в уравнение y-y1=k(x-x1), получим уравнение прямой, проходящей через точки М1 и M2:
в уравнение y-y1=k(x-x1), получим уравнение прямой, проходящей через точки М1 и M2:  .
.
в. параметрическое уравнение – 
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Зададим прямую a, указав лежащую на ней точку M1 (x1;y1) и направляющий вектор этой прямой  .
.
Возьмем произвольную точку плоскости M (x;y). Мы можем вычислить координаты вектора 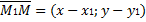 . Очевидно, что множество всех точек M (x;y) задают прямую, проходящую через точку M1 (x1;y1) и имеющую направляющий вектор
. Очевидно, что множество всех точек M (x;y) задают прямую, проходящую через точку M1 (x1;y1) и имеющую направляющий вектор  , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 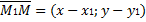 и
и  коллинеарны.
коллинеарны.

Необходимое и достаточное условие коллинеарности векторов 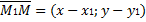 и
и  записывается в виде уравнения
записывается в виде уравнения  , где
, где 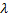 - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой. Векторно-параметрическое уравнение прямой в координатной форме имеет вид
- некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой. Векторно-параметрическое уравнение прямой в координатной форме имеет вид  . Уравнения полученной системы
. Уравнения полученной системы  называются параметрическими уравнениями прямой на плоскости.
называются параметрическими уравнениями прямой на плоскости.
каноническое уравнение – 
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Нужно получить уравнение прямой a, если M1 (x1;y1) - некоторая точка прямой a и  - направляющий вектор прямой a.
- направляющий вектор прямой a.
Пусть M (x;y)- плавающая точка прямой a. Тогда вектор  является направляющим вектором прямой a и имеет координаты
является направляющим вектором прямой a и имеет координаты  . Очевидно, что множество всех точек M (x;y)на плоскости определяют прямую, проходящую через точку M1 (x1;y1) и имеющую направляющий вектор
. Очевидно, что множество всех точек M (x;y)на плоскости определяют прямую, проходящую через точку M1 (x1;y1) и имеющую направляющий вектор  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 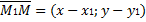 и
и  - коллинеарны.
- коллинеарны.

Равенство  в координатной форме имеет вид
в координатной форме имеет вид 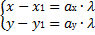 .
.
Если  и
и  , то мы можем записать
, то мы можем записать  .
.
Полученное уравнение вида  называют каноническим уравнением прямой на плоскости. Это уравнение также называют уравнением прямой в каноническом виде.
называют каноническим уравнением прямой на плоскости. Это уравнение также называют уравнением прямой в каноническом виде.
г*. уравнение прямой в отрезках – 
Пусть прямая пересекает ось в точке М1(  ), а ось
), а ось  - в точке М2 (
- в точке М2 (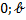 ). В этом случае уравнение имеет вид
). В этом случае уравнение имеет вид  , т. е.
, т. е.  . Это уравнение называется уравнением прямой в отрезках, так как числа
. Это уравнение называется уравнением прямой в отрезках, так как числа  и
и  указывают, какие отрезки отсекает прямая на осях координат.
указывают, какие отрезки отсекает прямая на осях координат.
полярное уравнение –  .
.
Положение прямой можно определить, указав расстояние  от полюса О до данной прямой и угол
от полюса О до данной прямой и угол  между полярной осью ОР и осью
между полярной осью ОР и осью  , проходящей через полюс О перпендикулярно данной прямой.
, проходящей через полюс О перпендикулярно данной прямой.
Для любой точки М ( ) на данной прямой имеем:
) на данной прямой имеем:
пр l  =
=  .
.
С другой стороны,
пр l  =|
=|  |
|  .
.
Следовательно,

Полученное уравнение и есть уравнение прямой в полярных координатах или полярное уравнение прямой.
нормальное уравнение прямой - 
Пусть прямая определяется заданием  и
и  . Рассмотрим прямоугольную систему координат Oxy. Введем полярную систему, взяв О за полюс и Ox за полярную ось. Уравнение прямой можно записать в виде
. Рассмотрим прямоугольную систему координат Oxy. Введем полярную систему, взяв О за полюс и Ox за полярную ось. Уравнение прямой можно записать в виде  , т. е.
, т. е.  .
.
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем:  ,
,  . Следовательно уравнение
. Следовательно уравнение  прямой в прямоугольной системе координат имеет вид
прямой в прямоугольной системе координат имеет вид  .
.
Это уравнение называется нормальным уравнением прямой.
Дата добавления: 2015-01-30; просмотров: 136 | Поможем написать вашу работу | Нарушение авторских прав |