Читайте также:
|
Требуется найти точку пересечения прямой L: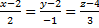 
с плоскостью Q: x+3y+5z-42=0.
Для этого нужно решить систему, состоящую из уравнений прямой и плоскости. Проще всего это сделать, записав уравнения прямой в параметрическом виде: L: 
.
Подставляя эти выражения для x, y и z в уравнение плоскости, получаем уравнение 
или 
; 
, и приведя подобные, мы получаем значение 
, но при условии, что прямая не параллельна плоскости, т. е. 
.
Подставляя найденное значение параметра 
в параметрические уравнения прямой, найдем координаты точки пересечения прямой с плоскостью: 
, т. е. точка О (4;1;7) – точка пересечения прямой L с плоскостью Q.
Рассмотрим случай, когда 
:
А) если 
, то прямая параллельна плоскости и пересекать ее не будет, т. е. уравнение решения не имеет.
Б) если 
, то уравнению удовлетворяет любое значение , любая точка прямой является точкой пересечения прямой и плоскости. Следовательно, прямая лежит на плоскости.
Таким образом, одновременное выполнение равенств 
является условием принадлежности прямой плоскости.
Дата добавления: 2015-01-30; просмотров: 136 | Поможем написать вашу работу | Нарушение авторских прав |