Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Уравнение линии в пространстве. Прямая в пространстве. Различные виды прямой в пространстве.

а. Каноническое уравнение -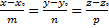

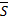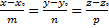Пусть вектор – направляющий вектор прямой L и M₀(x₀;y₀;z₀) – точка, лежащая на этой прямой. Вектор , где (x;y;z) – произвольная точка прямой L, параллелен вектору . Поэтому координаты вектора и вектора пропорциональны: . Эти уравнения называются каноническими уравнениями прямой в пространстве.

Чтобы получить последовательное доказательство, сперва нужно привести доказательство векторного уравнения прямой.

г.* векторное уравнение -

Пусть прямая L задана точкой M₀(x₀;y₀;z₀) и направляющим вектором . Возьмем на прямой L произвольную точку (x;y;z). Обозначим радиус-векторы точек M₀ и соответственно через и . Три вектора , и связаны соотношением .

Вектор , лежащий на прямой L, параллелен направляющему вектору 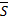, поэтому , где - скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки на прямой.

Векторное уравнение прямой можно записать в следующем виде .

Параметрическое уравнение –

Опираясь на предыдущее доказательство, заметим, что =(x;y;z), , , векторное уравнение прямой можно записать в виде . Отсюда следуют равенства .

Они называются параметрическими уравнениями прямой в пространстве.

б. Уравнение прямой в пространстве, проходящей через две заданные точки –

Пусть прямая L проходит через точки M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂). В качестве направляющего вектора 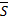можно взять вектор , т. е. 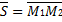. Следовательно , , . Поскольку прямая проходит через точку M₁(x₁;y₁;z₁), то, согласно каноническому уравнению, уравнение прямой имеет вид .

Эти уравнения называются уравнениями прямой, проходящей через две данные точки.

в. Общее уравнение прямой в пространстве (как линии пересечения плоскостей) –

Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.

Каждое из уравнений системы определяет плоскость. Если плоскости не параллельны (координаты векторов и не пропорциональны), то эта система определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. Уравнения этой системы называют общими уравнениями прямой.

От общих уравнений можно перейти к каноническим. Координаты точки на прямой L получаем из общих уравнений, придав одной из координат произвольное значение(например, ).

Так как прямая L перпендикулярна векторам и , то за направляющий вектор 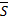прямой L можно принять векторное произведение : .