Читайте также:
|
Приведение общего уравнения прямой 
к каноническому уравнению прямой: если 
, то переносим слагаемое 
в правую часть равенства 
с противоположным знаком 
. В левой части равенства выносим А за скобки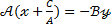 
. Полученное равенство можно записать как пропорцию вида 
.
Если 
, то оставляем в левой части общего уравнения прямой только слагаемое 
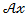, а остальные переносим в правую часть с противоположным знаком: 
. Теперь выносим в правой части равенства –B за скобки 
и записываем полученное равенство в виде пропорции 
.
Переход от общего уравнения прямой к параметрическим уравнениям прямой проводится в два этапа: сначала общее уравнение приводится к каноническому виду, а затем осуществляется переход от канонического уравнения прямой к параметрическим уравнениям прямой.
Разберем этот алгоритм при решении примера.
Нужно написать параметрические уравнения прямой, которая задана общим уравнением прямой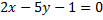 
.
Сначала приведем исходное общее уравнение прямой к каноническому уравнению прямой: 
.
Теперь принимаем левую и правую части полученного уравнения равными параметру Теперь принимаем левую и правую части полученного уравнения равными параметру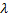 
: 
.
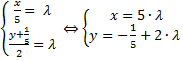Из общего уравнения прямой вида получить уравнение прямой с угловым коэффициентом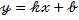 
возможно лишь тогда, когда 
.
Для этого в левой части общего уравнения прямой оставить только слагаемое 
: 
. Затем разделить обе части полученного равенства на число B, которое отлично от нуля, 
.
Чтобы получить уравнение прямой в отрезках вида 
из общего уравнения прямой переносим число С в правую часть равенства с противоположным знаком, делим обе части полученного равенства на –С, и в заключении переносим в знаменатели коэффициенты при переменных x и y: 
Чтобы привести общее уравнение прямой к нормальному виду нужно обе части равенства умножить на так называемый нормирующий множитель, который равен 
. Знак нормирующего множителя берется противоположным знаку слагаемого С. Если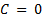 
, то знак нормирующего множителя не имеет значения и может быть выбран произвольно.
Для перехода к общему уравнению от уравнения прямой в отрезках и уравнения прямой с угловым коэффициентом достаточно просто собрать все слагаемые в левой части равенства:
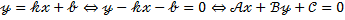
Каноническое уравнение прямой приводится к общему уравнению прямой с помощью следующих преобразований:
От параметрических уравнений прямой следует сначала перейти к каноническому уравнению прямой, а уже потом к общему уравнению прямо:
Дата добавления: 2015-01-30; просмотров: 106 | Поможем написать вашу работу | Нарушение авторских прав |