
Читайте также:
|

имеют вид:
 ;
;  .
.
Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.
Приведем формулы интегрального метода для смешанных моделей вида
 .
.
Эти формулы имеют вид:
 ;
;  ;
;  .
.
Для смешанных моделей вида

формулы интегрального метода – следующие:
 ;
; 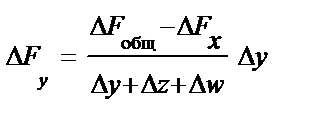 ;
;  ;
;  .
.
интегральный метод точен, дает единообразные результаты, не требует классификации факторов и применим к большинству видов детерминированных факторных моделей, поэтому при решении практических задач анализа нужно отдавать предпочтение именно ему, а не МЦП или МАР.
Заметим, что есть еще более точный метод решения прямой задачи факторного анализа для детерминированных моделей, чем интегральный. Это логарифмический метод. В логарифмическом методе неразложимый остаток распределяется между оценками влияния отдельных факторов не равными частями, а пропорционально силе влияния этих факторов на результирующий показатель.
Логарифмический метод имеет весьма ограниченную область применения, он применим только к мультипликативным факторным моделям, поэтому мы не будем приводить его формулы. Тем не менее, отметим еще одно положительное свойство этого метода. Он дает единообразные результаты при любом порядке факторов в модели, поэтому не требуется их предварительная классификация и расстановка.
Метод получил свое название из-за того, что его формулы получены способом логарифмирования.
Дата добавления: 2015-02-16; просмотров: 188 | Поможем написать вашу работу | Нарушение авторских прав |