
Читайте также:
|
Каждый треугольник имеет три высоты. Высоту, проведенную из вершины  на сторону
на сторону  , принято обозначать
, принято обозначать 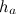 . Высоты треугольников или их продолжение пересекается в одной точке. В остроугольном треугольнике точка
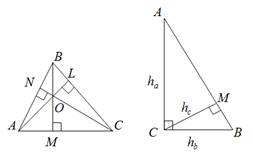
. Высоты треугольников или их продолжение пересекается в одной точке. В остроугольном треугольнике точка  пересечения высот находится внутри треугольника; в прямоугольном - в вершине прямого угла (совпадает с точкой
пересечения высот находится внутри треугольника; в прямоугольном - в вершине прямого угла (совпадает с точкой  ); в тупоугольном треугольнике - за пределами треугольника. Точка пересечения высот или их продолжений называется ортоцентром.
); в тупоугольном треугольнике - за пределами треугольника. Точка пересечения высот или их продолжений называется ортоцентром.

Задание. В треугольнике 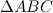 сторона
сторона  мм,
мм,  . Найти высоту, опущенную на сторону
. Найти высоту, опущенную на сторону 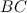 .
.
Решение. Обозначим искомую высоту 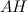 .
.

Для нахождения высоты 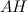 воспользуемся формулой
воспользуемся формулой

которая в наших обозначениях запишется следующим образом:

Подставим в последнее равенство исходные данные, получим


 (мм)
(мм)
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Как построить медиану треугольника?
Чтобы построить медиану треугольника, надо:
1) С помощью линейки найти и отметить середину стороны треугольника.
2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.
Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».
Сколько медиан имеет треугольник?
Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.
Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.
Биссектрисой треугольника называется отрезок, который соединяет вершину с противоположной стороной и делит соответствующий угол пополам.
Каждый треугольник имеет три биссектрисы.

На рисунке 1 в треугольнике  :
:  - биссектриса угла
- биссектриса угла  ,
,  - биссектриса угла
- биссектриса угла  ,
,  - биссектриса угла
- биссектриса угла  . Биссектрисы пересекаются в одной точке (на рисунке 1 точка
. Биссектрисы пересекаются в одной точке (на рисунке 1 точка  ), которая лежит в середине треугольника и называется инцентром.
), которая лежит в середине треугольника и называется инцентром.
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные к прилегающим сторонам:

Задание. В треугольнике 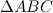 :
:  - биссектриса, сторона
- биссектриса, сторона  см,
см,  см, отрезок
см, отрезок  см. Найти длину отрезка
см. Найти длину отрезка  .
.
Решение. По свойству биссектрисы

Подставляя в это равенство исходные данные, получим
 (см)
(см)
Ответ.  см
см
Задачи на самостоятельное решение.
1. В прямоугольном треугольнике биссектриса, проведенная из вершины прямого угла, делит гипотенузу в отношении 3: 2, а высота делит гипотенузу на отрезки, один из которых на 20 больше другого. Найти площадь треугольника.
2. Стороны прямоугольного треугольника образуют геометрическую прогрессию. Найти значение выражения (6 + 2√5)1/2 · sin α, где α – меньший угол треугольника.
3. В прямоугольном треугольнике катеты равны 24√2 и 7√2. Найти расстояние от вершины прямого угла до центра вписанной в этот треугольник окружности.
4. Площадь прямоугольного треугольника равна 6√3. Найти его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1: 2.
5. Стороны треугольника равны √5; 2; 3. Найти квадрат расстояния от вершины меньшего угла треугольника до точки пересечения его биссектрис.
6. В прямоугольном треугольнике длины медиан, проведенных из вершин острых углов, равны √34 и √11. Найти длину гипотенузы.
Дата добавления: 2015-04-11; просмотров: 203 | Поможем написать вашу работу | Нарушение авторских прав |