Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Изменения энтропии в обратимых процессах.

Переход теплоты от одного тела к другому при бесконечно малом понижении температуры яв­ляется обратимым процессом, так как направление перехода тепла можно изменить на обратное посредством бесконечно малого изменения темпера­туры одного из тел. Примерами изотермических процессов, которые могут быть обращены путем бесконечно малого изменения температуры, служат плавление твердого вещества в точке плавления и испарение жидкости при постоянном парциальном давлении вещества, равном давлению его пара. Для этих процессов можно рассчитать изменение энтропии. Так как температура постоянна, интегрирование уравнения (5.3) дает

(5.4)

где q_обр – количество тепла, поглощенное в обратимом процессе.

Для моля вещества при постоянных температуре и давлении

(5.5)

Пример 2.

н-Гексан кипит при 68,7 °С, теплота испарения его при этой темпе­ратуре и постоянном давлении равна 6 896 кал/молъ. Если жидкость при испарении превращается в пар, насыщенный при 68,7 °С, то процесс обратим и изменение энтро­пии на моль вещества дается уравнением

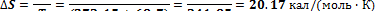
Мольная энтропия пара всегда больше, чем мольная энтропия жид­кости, с которой пар находится в равновесии, а мольная энтропия жид­кости всегда больше, чем мольная энтропия твердого вещества в точке плавления.

В соответствии с представлением об энтропии как о мере беспорядка в системе движение молекул газа более беспорядочно, чем моле­кул жидкости, а движение молекул жидкости более беспорядочно, чем молекул твердого вещества.

Тот же метод применяется для расчета энтропии возгонки, плавления или изменения энтропии при переходе между двумя формами твердого ве­щества. Поскольку количество теплоты, полученное системой, равно по­тере теплоты внешней средой, изменение энтропии среды равно взятому с обратным знаком изменению энтропии системы.

Для системы и внешней среды, взятых вместе, ΔS = 0, если передача тепла происходит обратимо.

Увеличение энтропии вещества за счет повышения его температуры можно рассчитать, поскольку изменение температуры может быть прове­дено обратимо.

Теплота, поглощенная при каждом бесконечно малом из­менении, равна теплоемкости С, умноженной на дифференциал темпера­туры dT,тогда

(5.6)

Интегрируя уравнение (6) в пределах от Т₁ до Т₂, получим:

(5.7)
Если С не зависит от температуры, то

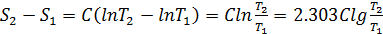(5.8)

Энтропия всегда увеличивается с повышением температуры. Это согласуется с усилением беспорядочности движения молекул при повыше­нии температуры. Уравнение (5.8) применимо при постоянном давлении или постоянном объеме. Если нагревание происходит при постоянном объ­еме, то пользуются теплоемкостью при постоянном объеме С_V; при по­стоянном давлении пользуются теплоемкостью при постоянном давле­нии С_P.

Если теплоемкость изменяется в процессе нагревания, то в уравнение (5.7) перед интегрированием можно ввести эмпирическое соотношение зависимости теплоемкости от температуры.

Уравнение для расчета изменения энтропии моля идеального газа с изменением объема и температуры при постоянном давлении можно полу­чить, если записать первый закон термодинамики в дифференциальной форме:

(5.9)

Бесконечно малое изменение энтропии, сопровождающее бесконечно малые изменения температуры dT и объема dV, равно:

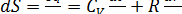(5.10)

Предполагая, что С_V не зависит от температуры и объема, получим при интегрировании

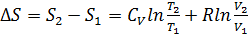(5.11)

Если объем остается постоянным, то уравнение (5.11) превращается в уравнение (5.8). Если постоянна температура, то

(5.12)

Как видно из уравнения (5.12), для десятикратного увеличения объема идеального газа

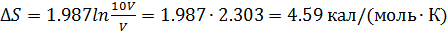
Энтропия газа будет изменяться на эту величину независимо от того, обратимо или необратимо будет происходить расширение, потому что ΔS зависит только от энтропии начального и конечного состояний.