Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Химическое равновесие

Наиболее важные понятия термодинамики - «теплота процес­са» и «работа». Преобразование теплоты в работу или работы в теп­лоту осуществляется обычно в термодинамическом процессе по­средством рабочего тела. Термодинамическая система называется однородной, если во всех частях системы свойства одинаковы. Совокупность физических свойств рабочего тела (или термодина­мической системы) в рассматриваемых условиях называется со­стоянием тела (или системы). Величины, характеризующие состо­яние термодинамической системы, называют термодинамическими параметрами. К ним относят температуру, давление, удельный объем, плотность, молярный объем, удельную внутреннюю энер­гию и др.

Термодинамические параметры делят на экстенсивные и ин­тенсивные. Величины, пропорциональные массе (или количеству вещества) рассматриваемого рабочего тела или термодинамической системы, называются экстенсивными это – объем, внутренняя энергия, энтальпия, энтропия и т. п. Экстенсивные параметры об­ладают свойством аддитивности. Интенсивные величины не зависят от массы термодинамиче­ской системы, и только они служат термодинамическими параметрами состояния. Это – температура, давление, а также экстенсивные величины, отнесенные к единице массы, объема или количества вещества. Изменение интенсивных параметров для ускорения хи­мико-технологических процессов называется интенсификацией.

Под воздействием подвода или отвода энергии в форме тепло­ты или работы происходит изменение состояния термодинамиче­ской системы (значений термодинамических параметров), назы­ваемое термодинамическим процессом. Процессы, представляющие собой непрерывный ряд равновесных состояний, называют равно­весными. При этом равновесным считают состояние, в которое приходит система при постоянных внешних условиях, характери­зуемое неизменностью во времени термодинамических парамет­ров и отсутствием в системе потоков вещества и теплоты.

Устойчивое равновесие характеризуется следующими общими условиями:

1) неизменностью равновесного состояния системы во времени при постоянных внешних условиях;

2) подвижностью равновесия (са­мопроизвольным восстановлением состояния равновесия после сня­тия внешнего воздействия, вызвавшего отклонение системы от поло­жения равновесия);

3) динамическим характером равновесия, т.е. установлением и сохранением равновесия вследствие равенства ско­ростей прямого и обратного процессов; 4) возможностью подхода к состоянию равновесия с двух противоположных сторон;

5) мини­мальным значением энергии Гиббса G в изобарно-изотермических и энергии Гельмгольца F в изохорно-изотермических процессах.

Изобарный и изохорный потенциалы.

Мы разобрали такие понятия как энтальпия, изобарная и изохорная теплоемкость, введением энтропии был завер­шен ряд термодинамических функций, необходимых для расчетов. Однако удобно ввести еще три функции: G, F и μ, которые обладают весьма по­лезными свойствами. Энтропия S дает критерий равновесия для изолиро­ванной системы, изобарный потенциал G – для системы при постоянных температуре и давлении, изохорный потенциал F – при постоянных температуре и объеме, химический потенциал μ является интенсивной величиной, определяющей направление химического или физи­ческого процесса.

Изобарный потенциал G (энергия Гиббса) определяется через другие термодинамические функции соотношением

G = H – TS = U + PV – TS (5.25)

Изменение изобарного потенциала при переходе из состояния 1 в со­стояние 2 равно:

G₂ – G₁ = (U₂ – U₁) + (P₂V₂ – P₁V₁) – (T₂S₂-T₁S₁)

ΔG = ΔU + Δ(PV) – Δ(TS) = ΔH – Δ(TS) (5.26)

При постоянных давлении и температуре

ΔG = ΔU + PΔV – TΔS (5.27)

Из курса термодинамики известно, что изменение внутренней энергии системы равно количеству теплоты подведенной к системе, за вычетом работы совершенной системой или ΔU = q – A. Следовательно, получим

ΔG = ΔU = q – A + PΔV – TΔS (5.28)

Если процесс проводится обратимо и теплота q переносится от тела с бесконечной теплоемкостью, и имеющего температуру Т, одинаковую с температурой системы, то q = TΔS и работа А = А_обр. Тогда можно записать

- ΔG = А_обр – PΔV (5.29)

Таким образом, когда процесс происходит обратимо при постоянных температуре и давлении уменьшение термодинамического потенциала равно максимальной работе А_обр за вычетом работы расширения PΔV.

Если процесс проводится обратимо и теплота q переносится от тела с бесконечной теплоемкостью, и имеющего температуру Т, одинаковую с температурой системы, то TΔS > q. Подстановка в уравнение (5.28) показывает, что

- ΔG > А_обр – PΔV (5.30)

Таким образом, для необратимого процесса при постоянных темпера­туре и давлении уменьшение изобарного потенциала больше, чем макси­мальная работа, которая может быть получена помимо работы расши­рения.

Изохорный потенциал F определяется через другие термодинамические функции следующим образом:

F = U – TS или ΔF = ΔU – Δ(TS) (5.31)

Полагая температуру Т постоянной и подставляя в уравнение (5.31) уравнение изменения внутренней энергии, можно показать, что

- ΔF = А_обр (5.32)

Таким образом, уменьшение изохорного потенциала равно максимальной работе, которую можно получить при изотермическом процессе.

Независимо от обратимости или необратимости данного процесса функция F изменяется на одну и ту же величину. Однако для того чтобы определить уменьшение функции F для данного процесса, необходимо измерить работу обратимого процесса.

Критерии химического равновесия.

Пытаясь найти термодинамический критерий самопроизвольности химических реакций Бертело в 1879 г. пришел к неправильному выводу, что самопроизвольны лишь те реакции, при которых выделяется тепло. Открытие самопроизвольных реакций, при которых тепло поглощается, доказало неправильность этого заключения. Можно показать, что изотермический процесс при постоянном давлении протекает самопроизвольно, если G уменьшается; изотермический же процесс при постоянном объеме протекает самопроизвольно, если умень­шается F.

Для практических целей весьма важно знать – в равновесном или только в метастабильном состоянии находится система. Под равновес­ным, мы имеем в виду такое состояние, в котором система не может под­вергаться самопроизвольным изменениям. Иными словами, при равно­весии любое бесконечно малое изменение в системе должно быть обрати­мым, так как любое необратимое изменение привело бы к смещению пер­воначального равновесия.

Рассмотрим систему, находящуюся в контакте с тепловым резервуаром при температуре Т, в которой происходит бесконечно малое необратимое изменение и совершается только работа расширения, δq – количество теплоты, которой система обменивается с резервуаром. Ввиду того что процесс необратим, dS для системы больше, чем δq/Т, как это было показано ранее, т. е.

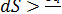
Так как TdS больше, чем δq, то разность:

(5.33)

Поскольку производится только работа расширения, постольку δq = dU + PdV. Подставляя это выражение в уравнение (5.33), получим

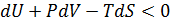(5.34)

Это неравенство справедливо во всех случаях, когда совершается толь­ко работа расширения. Если объем и энтропия системы постоянны, то

(5.35)

Следовательно, в системе при постоянном объеме для любого необра­тимого процесса, происходящего без изменения энтропии, внутренняя энергия уменьшается. Это соответствует обычному условию, что для кон­сервативной механической системы стабильным является состояние с наименьшей энергией.

Если в ходе бесконечно малого необратимого изменения объем и внутреннюю энергию системы поддерживать постоянными, то неравенство (5.34) переходит в

(5.36)

Объем и внутреннюю энергию системы можно поддерживать постоян­ными путем изолирования системы. Таким образом, как было сказано ранее, энтропия при необратимых процессах в изолированной системе увеличивается. Следует помнить, что неравенства (5.34), (5.35) и (5.36) применимы лишь к системам, в которых совершается только работа расширения.

Если система незамкнута (открытая), то необходимо рассматривать изменение энтропии в контактирующих с ней системах. Эти добавочные изменения энтропии учитываются автоматически, когда функции F и G применяются в соответствующих условиях.

Если во время бесконечно малых измене­ний объем постоянен, то неравенство (5.34) принимает вид:

(5.37)

(5.38)

Подставляя F = U – TS, получаем

(5.39)

Таким образом, в необратимом процессе при постоянных Т u V изо­хорный потенциал F уменьшается.

Обычно в лаборатории физические процессы и химические реакции проводят при постоянных давлении и температуре. Когда Р и Т постоян­ны, неравенство (5.34) принимает вид:

(5.40) Вводя G = U + PV - TS, получим

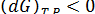(5.41)

Таким образом, в случае необратимого процесса при постоянных Т и Р, если совершается только работа расширения, изобарный потенциал G уменьшается.

Если рассматривавшиеся выше процессы обратимы, то все знаки неравенства нужно заменить знаками равенства в соответствии с уравнением (5.1). Условия для необратимости и обратимости процессов, в которых совершается только работа расширения, даны в таблице.