Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Критерии необратимости и обратимости процессов, при которых не совершается работа или совершается только работа расширения

Для обратимых процессов	Для необратимых процессов	Для обратимых процессов	Для необратимых процессов

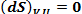
Каждая строка в таблице представляет собой математическую формулировку второго за­кона термодинамики. Так как изобарный потенциал в необратимом про­цессе при постоянных Т и Р уменьшается, то в конечном равновесном со­стоянии он становится минимальным, т. е. dG = 0 для любого бесконечно малого изменения. Мы можем представить себе процесс, протекающий при равновесии. Например, можно представить испарение бесконечно малого количества воды, находящейся в равновесии с насыщенным паром при постоянных температуре и давлении. Для такого процесса dG = 0.

Те же самые соотношения могут применяться не только к бесконечно малым, но и к конечным изменениям, при этом d заменяется на Δ. Однако следует помнить, что самопроизвольные процессы всегда приводят к минимуму (в случае изобарного потенциала при постоянных Т и Р) или к максимуму (вслучае энтропии S изолированной системы) функции, а не к какому-нибудь другому ее значению, даже если переход к этому новому значению удовлетворял бы соответствующему неравенству.

Приведенные рассуждения ограничивались системами, которые не имели возможности совершать какую-либо другую работу, кроме работы расширения. Если система включает в себя гальванический элемент, то может производиться электрическая работа, и критерий равновесия сле­дует изменить.

Хотя эти критерии показывают, является ли некоторый процесс самопроизвольным, однако они не дают еще основания сделать вывод о том, что изменения будут происходить с заметной скоростью.

Например, смесь 1 моль углерода с 1 моль кислорода при 1 атм и 25°С имеет больший изо­барный потенциал, чем 1 моль двуокиси углерода при 1 атм и 25°С; следо­вательно, имеется возможность образования двуокиси углерода из угле­рода и кислорода при данных постоянных температуре и давлении. Эта реакция теоретически возможна, хотя углерод может существовать в контакте с кислородом очень долгое время. Процесс, обратный самопро­извольному, конечно, является несамопроизвольным. Так, разложение двуокиси углерода при комнатной температуре, сопровождающееся уве­личением изобарного потенциала, - несамопроизвольный процесс. Он может происходить только под внешним воздействием, например при на­гревании до очень высокой температуры, при которой изменение изобар­ного потенциала поменяет знак на противоположный.

Изобарный потенциал как критерий равновесия.

Рассмотрение изо­барного потенциала как критерия равновесия или самопроизвольности процесса при постоянных температуре и давлении можно пояснить на примере смеси льда и воды. И лед, и вода имеют одинаковый мольный изобарный потенциал при 0° и 1 атм. В этих условиях лед не плавится, а вода не замерзает ΔG = 0. С другой стороны, мольный изобарный потенциал для воды, переохлажденной до -10°С, больше, чем для льда при -10°С (давление 1 атм). Переход воды в лед в этих условиях сопровождается изменением изобарного потенциала и, следовательно, является самопроизвольным переходом ΔG < 0. Переход в обратном направлении, т. е. превращение льда в воду при -10°, не может протекать самопроизвольно, потому что он сопровождался бы увеличением изобарного потенциала, т. е. ΔG > 0.

Для изотермического процесса получим изменение термодинамического потенциала из уравнения (5.26):

ΔG = ΔH – TΔS (5.42)

Это очень важное уравнение. ΔH и ΔS можно определять прямыми калориметрическими измерениями, азатем рассчитывать ΔG. Изменение изобарного потенциала использу­ется в расчетах электродвижущих сил электрохимических элементов и констант равновесия химических реакций.

При постоянных температуре и давлении положение равновесия определяется двумя противоположными тенденциями:

во-первых, происходит максимально возможное уменьшение энергии,

во-вторых, максимально возможно увеличивается энтропия.

Поскольку функция G в положении равновесия при постоянных температуре и давлении минимальна, то разность H - TS также должна быть минимальной при равновесии.

При смешении двух идеальных газов ΔH = 0, при этом изменение изобарного потенциала можно рассчитать из уравнений (5,42) и (5.17):

Δ G = RT∙(X₁lnX₁ + X₂lnX₂) (5.43)

Вследствие того, что X_i < 1, очевидно, что величина Δ G при смешении идеальных газов при постоянных температуре и давлении всег­да отрицательна.