Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Интервальное оценивание параметров распределений

Доверительный интервал. Доверительная вероятность
Точечная оценка неизвестного (оцениваемого) параметра распределения (фактически — приближенное значение параметра) является случайной величиной. Если известно ее распределение (или хотя бы дисперсия), то можно указать пределы, в которых с достаточно большой вероятностью лежит неизвестное значение параметра. Важно понимать, что пользоваться полученными значениями пределов можно только тогда, когда они не зависят от самого оцениваемого параметра.
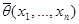Зададимся достаточно малой с практической точки зрения вероятностью a и рассмотрим выборку x 1, x 2, …, xn из генеральной совокупности, отвечающей случайной величине x, функция распределения которой , а q — неизвестный параметр. Предположим, что удалось найти две такие функции и , что

· при всех x 1, x 2, …, xn;

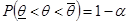· при любых значениях параметра q.

Доверительный интервал для математического ожидания нормально распределен- ной генеральной совокупности Пусть случайная величина нормально распределена. По выборке длины n найдем вы- борочное среднее x¯, а с помощью функции Stdev выборочное стандартное отклонение S. Затем найдем величину t:= qt 1 + γ 2, n − 1, а затем и точность оценки, величину ε — половину длины доверительного интервала ε = t S √ n. Окончательно, доверительный интервал для математического ожидания при неиз- вестной дисперсии имеет вид Iγ = (¯x − ε, x¯ + ε)

56 Понятие оценки. Свойства оценок. Виды оценок. Для установления качества оценки используют три основные свойства и рассматривают несмещенные оценки, состоятельные оценки и эффективные оценки.

Для того, чтобы определить эти свойства, необходимо предварительно ввести понятие статистики. Под статистикой будем понимать функцию от выборки случайной величины . Следует отметить, что функция 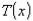сама является случайной величиной. Если статистика 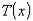позволяет оценить

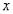некоторую характеристику случайной величины , то говорят, что статистика оценивает . Например, статистика, оценивающая дисперсию случайной величины имеет вид:.Статистика 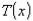называется несмещенной оценкой параметра , если математическое ожидание оценки равняется оцениваемому параметру:Статистика 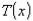называется эффективной оценкой параметра , если среднеквадратическая ошибка данной оценки является наименьшей среди всех возможных оценок:Статистика 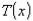называется состоятельной оценкой параметра параметра , если с ростом размера выборки оценка стремиться по вероятности к оцениваемому параметру:

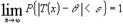при любом сколь угодно малом