Читайте также:
|
ТЕОРЕМЫ О ПРЕДЕЛАХ
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля,
еорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0. –
Точки разрыва функции и их классификация
‚Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если х = х 0 - точка разрыва функции y = f (x), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции.
Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.
Теорема 1. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель не равен нулю).
Теорема 2. Пусть функции u = φ (x) непрерывна в точке х 0, а функция y = f (u) непрерывна в точке u = φ (x0). Тогда сложная функция f (φ (x)), состоящая из непрерывных функций, непрерывна в точке х 0.
Теорема 3. Если функция y = f (x) непрерывна и строго монотонна на [ a;b ] оси Ох, то обратная функция у = φ (x) также непрерывна и монотонна на соответствующем отрезке [ c; d ] оси Оу.
_ Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
5 Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
| 
| 
| 
| 
| 
| 
|
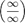
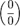
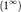
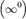
(Здесь 
— бесконечно малая величина, а 
— бесконечно большая величина)
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов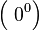 
, 
, 
пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту. Первый замечательный предел
Первым замечательным пределом именуют следующее равенство:
limα→0sinαα=1(1)
Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 00. Вообще говоря, в формуле (1) вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:
1. Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 00.
2. Выражения под знаком синуса и в знаменателе совпадают.
7 На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
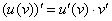
Разбираемся. Прежде всего, обратим внимание на запись 
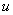. Здесь у нас две функции – 
и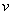 
, причем функция 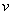, образно говоря, вложена в функцию 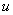. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию 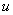я буду называть внешней функцией, а функцию 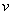– внутренней (или вложенной) функцией.
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал
8 Производные высшего порядка явно заданной функции
Пусть функция y = f (x) имеет конечную производную f ' (x) в некотором интервале (a, b), т.е. производная f ' (x)также является функцией в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции f, которая обозначается в виде
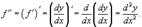
Дата добавления: 2015-01-30; просмотров: 85 | Поможем написать вашу работу | Нарушение авторских прав |