Читайте также:
|
Нехай на відрізку 
задано функцію 
. Фігура, яка обмежена графіком даної функції і відрізками прямих 
називається криволінійною трапецією (рис. 8.2).
Рис. 8.2.
Треба обчислити площу 
цієї трапеції. Зауважимо, що у загальному випадку ця трапеція – саме криволінійна фігура, і лише у частинних випадках, коли функція 
стала, або лінійна (тобто її графіком є пряма лінія) ця фігура прямолінійна, і ми можемо використати відомі з елементарної геометрії формули для площ прямокутника та трапеції.
Розіб’ємо відрізок 
за допомогою довільно обраних точок
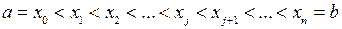
на 
частинних відрізків 
. На кожному з них візьмемо довільну точку 
і побудуємо прямокутник, основою якого є відповідний частинний відрізок, а висота дорівнює 
(рис. 8.3).
Рис. 8.3
З рис. 8.3. ми бачимо, що шукана площа наближено дорівнює сумі площ всіх отриманих прямокутників. Знайдемо цю суму. Очевидно, вона дорівнює:
, (8.1.1) де 
– довжина відрізка 
. Тобто 
. За рахунок чого можна було б збільшити точність цієї формули? Здається за рахунок збільшення кількості частинних відрізків, тобто числа . Але справа в тому, що кількість прямокутників можна збільшувати не на всьому відрізку , а тільки на деякій його частині (наприклад половині його), залишаючи кількість частинних відрізків на решті відрізка незмінним. І тоді очевидно, що ми не отримаємо підвищення точності. Тому треба йти іншим шляхом. А саме зменшувати всі величини 
. Фактично можна зменшувати 
. Зрозуміло, що тоді автоматично буде збільшуватися. І за площу криволінійної трапеції природно вважати границю послідовності площ ступінчатих фігур, якщо максимальна з довжин частинних відрізків прямує до нуля:
. (8.1.1)
Дата добавления: 2015-09-11; просмотров: 116 | Поможем написать вашу работу | Нарушение авторских прав |