Читайте также:
|
Теорема Ролля. Пусть функция 
удовлетворяет следующим условиям:
1) непрерывна на отрезке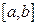 
;
2) дифференцируема на интервале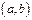 
;
3) на концах отрезка принимает разные значения, т.е.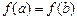 
.
Тогда внутри отрезка существует по крайней мере одна точка 
, в которой производная функции равна нулю: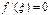 
.
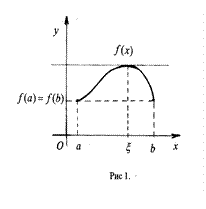
Геометрический смысл теоремы Ролля. При выполнении условий теоремы внутри отрезка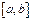 
найдется точка , в которой касательная, проведенная к графику функции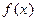 
, параллельна оси 
(см. рис. 1). Таких точек на интервале 
может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Замечание. Пусть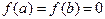 
. Тогда 
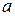и 
– нули функции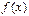 
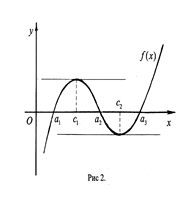
, и между ними найдется такая точка , что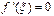 
. Таким образом, из теоремы Ролля следует, что между нулями дифференцируемой функции находится хотя бы один нуль производной (см. рис. 2).
Теорема Роля является частным случаем теоремы Лагранджа.
Теорема Лагранжа. Пусть функция 
удовлетворяет следующим условиям:
1) непрерывна на отрезке 
;
2) дифференцируема на интервале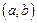 
.
Тогда внутри отрезка существует по крайней мере одна точка , в которой выполняется равенство: 
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
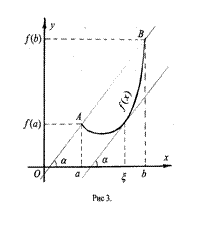На рис (см. рис. 3) хорда AB – отрезок, соединяющий точк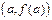и 
и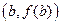 
. Величина 
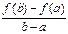равна тангенсу угла наклона прямой AB.
Геометрический смысл теоремы Лагранжа заключается в том, что при выполнении условий теоремы внутри отрезка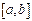 
найдется точка , в которой касательная, проведенная к графику функции 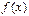, параллельна хорде AB. Таких точек может быть и несколько, но одна существует точно.
Следствие. При выполнении условий теоремы Лагранжа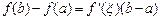 
.
Эту формулу называют формулой конечных приращений.
Дата добавления: 2015-09-11; просмотров: 27 | Поможем написать вашу работу | Нарушение авторских прав |