Читайте также:
|
1. Если функция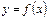 
непрерывна на отрезке 
, то она ограничена на этом отрезке. (рис. 1.1)
2. Если функция 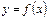непрерывна на отрезке , то она достигает на этом отрезке наименьшего значения 
и наибольшего значения 
(теорема Вейерштрасса). (рис. 1.2)
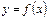3. Если функция непрерывна на отрезке и значения ее на концах отрезка 
и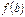 
имеют противоположные знаки, то внутри отрезка найдется точка 
такая, что 
. (Теорема Больцано-Коши.)
Пример. Исследовать на непрерывность и найти точки разрыва функции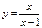 
. Установить характер разрыва.
Решение. При 
функция не определена, следовательно, функция в точке 
терпит разрыв: 
, а 
. Так как односторонние пределы бесконечны, то 
- точка разрыва второго рода.
Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
Дата добавления: 2015-09-11; просмотров: 79 | Поможем написать вашу работу | Нарушение авторских прав |