Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Точностные оценки и сравнение формул интегрирования.

Метод Симпсона (парабол).

При замене подынтегральной функции интерполяционным многочленом второй степени и четном числе 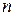интервалов разбиения квадратурная формула преобразуется к виду

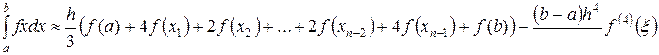
Погрешность усечения формулы Симпсона можно оценить при наличии на отрезке 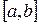непрерывной четвертой производной подынтегральной функции.

Формула парабол является точной для полиномов до третьей степени включительно, так как для них . Геометрическая интерпретация метода представлена на рис. 2.4.

Рис. 2.4.

Точностные оценки и сравнение формул интегрирования.

Оценка погрешности усечения рассмотренных формул численного интегрирования по выражениям для остаточных членов часто оказывается малоэффективной из-за трудностей оценки производных высокого порядка подынтегральных функций. В силу этого на практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов, состоящему в следующем. Задают значение допустимой погрешности и начальное число интервалов разбиения. Вычисляют величину интеграла 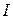по выбранной квадратурной формуле при числе интервалов и 2 (соответственно и ). По правилу Рунге оценивается погрешность приближенного значения интеграла

- для формулы Симпсона;

Если , количество интервалов разбиения увеличивают вдвое, т.е. значения интеграла вычисляются для последовательных значений . Вычисления заканчиваются при выполнении условия .

Этот прием позволяет осуществить автоматический выбор шага при заданной точности интегрирования. В формулах трапеций и Симпсона при удвоении числа интервалов разбиения нет необходимости вычислять значения подынтегральной функции заново во всех узлах, так как все узлы при числе интервалов 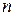являются узлами и при числе интервалов .

Интегрирование по квадратурным формулам сопровождается также ошибками округления. Они носят случайный характер, но с увеличением числа интервалов разбиения 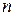возрастают в среднем пропорционально . Вследствие этого общая погрешность, равная сумме погрешностей усечения и округления, с ростом числа интервалов разбиения уменьшается за счет уменьшения ошибки усечения лишь до некоторого значения 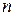. Затем погрешности округления преобладают и общая погрешность увеличивается.

В результате не для всякой функции можно получить результат с заданной погрешностью. Поэтому в программе может быть предусмотрено сообщение пользователю о недостижимости заданной точности. Интеграл при этом вычисляется с максимально возможной точностью, а программа выдает эту реальную точность.