
Читайте также:
|
Доказать, что  не имеет предела в точке 0.
не имеет предела в точке 0.

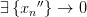




Вывод: последовательность по Гейне не имеет предела.
Бесконечно большая последовательность[править]
Определение. Последовательность  называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при
называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при  все элементы
все элементы  этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству  .
.
Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3,... 1, n,... не является бесконечно большой, так как при A > 1 неравенство  не выполняется для
не выполняется для  с нечетными номерами.
с нечетными номерами.
Бесконечно малая последовательность[править]
Определение. Последовательность  называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при
называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при  все элементы
все элементы  этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству  .
.
Любая бесконечно малая последовательность является ограниченной [1].
| Свойства бесконечно малых последовательностей |   
|
Свойство 1. Произведение бесконечно малой последовательности  и ограниченной последовательности и ограниченной последовательности  есть бесконечно малая последовательность есть бесконечно малая последовательность  . Доказательство. Ограниченность последовательности . Доказательство. Ограниченность последовательности  означает, что означает, что  для всех для всех  , где B – некоторое положительное число. Выберем сколь угодно малое число ε > 0. Согласно определению бесконечно малой последовательности существует такой номер N, начиная с которого величины , где B – некоторое положительное число. Выберем сколь угодно малое число ε > 0. Согласно определению бесконечно малой последовательности существует такой номер N, начиная с которого величины  становятся меньше любого положительного числа и, в частности, становятся меньше любого положительного числа и, в частности,  . Тогда . Тогда
 для всех n > N, что доказывает утверждение. Следствие. Умножиение бесконечно малой последовательности на любое число дает бесконечно малую последовательность.
Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая. Доказательство. Рассмотрим сначала сумму двух бесконечно малых величин
для всех n > N, что доказывает утверждение. Следствие. Умножиение бесконечно малой последовательности на любое число дает бесконечно малую последовательность.
Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая. Доказательство. Рассмотрим сначала сумму двух бесконечно малых величин 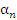 и и  . Пусть ε – произвольное положительное число. Тогда существуют номер . Пусть ε – произвольное положительное число. Тогда существуют номер  , начиная с которого бесконечно малые величины , начиная с которого бесконечно малые величины 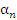 становятся меньше числа становятся меньше числа  : :
 Аналогично,
Аналогично,
 Обозначим символом N наибольший из номеров
Обозначим символом N наибольший из номеров  и и  . Тогда для всех номеров n > N выполняется неравенство . Тогда для всех номеров n > N выполняется неравенство
 выражающее справедливость доказываемого утверждения. Переходя к случаю суммы произвольного конечного числа бесконечно малых величин, заметим, что любая пара бесконечно малых в этой сумме может быть представлена одной бесконечно малой. Затем каждая пара полученных бесконечно малых может быть заменена одной бесконечно малой и так далее, что в конечном итоге позволит свести рассматриваемую сумму к единственной бесконечно малой.
выражающее справедливость доказываемого утверждения. Переходя к случаю суммы произвольного конечного числа бесконечно малых величин, заметим, что любая пара бесконечно малых в этой сумме может быть представлена одной бесконечно малой. Затем каждая пара полученных бесконечно малых может быть заменена одной бесконечно малой и так далее, что в конечном итоге позволит свести рассматриваемую сумму к единственной бесконечно малой.
|
Дата добавления: 2015-09-10; просмотров: 113 | Поможем написать вашу работу | Нарушение авторских прав |