Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Подстановки Эйлера.

Интегралы вида могут быть приведены к интегралу от рациональной функции с помощью подстановок Эйлера.

Первая подстановка Эйлера применима, если

Из указанной подстановки имеем , .

Пример 43. =

Замечание. При рационализация интеграла может быть достигнута с помощью подстановки , где комбинация знаков произвольна.

Вторая подстановка Эйлера применима при Из указанной подстановки получаем:

Пример 44 (см.пример 43).

Третья подстановка Эйлера применимавсякий раз, когдаквадратный трехчлен имеет действительные корни (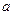 - любое число, отличное от нуля).

Пусть и корни квадратного трехчлена . Тогда

из подстановки имеем

Пример 45. J =

Подкоренное выражение положительно при 1< <2. Тогда, полагая

, имеем

J=

3.2.2. Интегрирование выражений вида .

Указанные выражения являются частными случаями выражения . Для интегрирования первого из этих выражений может быть применен метод неопределенных коэффициентов:

= ,

где коэффициенты многочлена и число определяют следующим образом.

Обе части последнего равенства дифференцируют по и результат умножают на : = ,

Далее сравнивают коэффициенты при одинаковых степенях .

Пример 46. =

Умножаем обе части равенства на .

= .

Приравниваем коэффициенты при одинаковых степенях

=

Замечание. Вычисление интеграла

умножением и делением на сводится к вычислению интеграла .