Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Различные обобщения уравнения Эйлера. Уравнение Пуассона-Эйлера и Остроградского.

Функционалы с производными высшего порядка

Рассмотрим сначала случай, когда подинтегральная функция содержит производные до второго порядка, и соответствующую вариационную задачу с закреплёнными концами:

, , , (2)

В этой задаче необходимо взять четыре условия закрепления, т.е

в два раза больше, чем порядок старшей производной в функционале J(y).

Вычисляя вариацию функционала (1) аналогично тому, как это

было сделано ранее, убеждаемся, что выражение для δI(y, δy) содер-

жит дополнительное слагаемое, именно, в отличие от примера 2.8,

здесь имеем

Отметим теперь, что в качестве области определения D(I) = X функционала J(y) нужно выбрать такие функции из , которые удовлетворяют краевым условиям (2). Тогда, очевидно, приращения δy(x) должны удовлетворять краевым условиям

, (4)

Применим к функционалу (3) приём интегрирования по частям, причём для второго слагаемого, как и раньше, один раз, а для третьего — два раза. При этом учтём условия (4). Тогда необходимое условие экстремума приводит к соотношению

Здесь предполагается, что функция F(x, y, y’, y’’) имеет непрерывные производные по своим аргументам вплоть до четвёртого порядка. Тогда выражение в скобках (5) — непрерывная функция, если искомая функция y = y(x) четырежды непрерывно дифференцируема, и по основной лемме вариационного исчисления из (5) получаем, что y = y(x) должна быть решением уравнения

, (6)

которое называют уравнением Эйлера-Пуассона.

Уравнение Эйлера-Пуассона представляет собой обыкновенное дифференциальное уравнение четвёртого порядка, его общее решение содержит четыре произвольных постоянных, которые находятся из четырёх краевых условий (2).

Функционалы от функций нескольких переменных

Рассмотрим для определённости случай, когда аргументом функционала является функция двух переменных z = z(x, y), заданная в некоторой области Ω ⊂

Функционал I{z}, содержащий саму функцию и ее первые частные производные

, имеет вид

Для простейшей вариационной задачи на контуре Γ= ∂Ω следует задать краевое условие Дирихле

где –известна.

Здесь, очевидно, в качестве области определения D(J) = X функционала J(z) следует взять множество

где - множество непрерывно дифференцируемых функций в замыкании области Ω.

Если (x, y) — решение вариационной задачи, а z(x, y) — любая другая функция из D(J), то

δz = z(x, y) − (x, y), δz = 0 (на Γ).

Воспользуемся формулой вычисления вариации функционала J(z):

Теорема. Пусть F = F(x, y, z, p, q) — дважды непрерывно дифференцируемая функция по всем своим аргументам. Если z(x, y) ∈ D(J) даёт экстремум функционалу J(z), то она является решением уравнения

(2)

называемым уравнением Эйлера-Остроградского.

Доказательство. Воспользуемся соотношениями

,

запишем второе и третье слагаемое (5.12) в виде повторного интеграла и осуществим интегрирование по частям во внутреннем интеграле. Например,

Аналогично для последнего слагаемого в (1) имеем

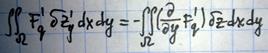
Поэтому, приравнивая нулю правую часть (1), т.е. вариацию

функционала J(z) и учитывая приведенные формулы, будем иметь

(3)

∀ , (на Γ= ∂Ω)

Теперь можно воспользоваться основной леммой вариационного исчисления для функций уже не одной, а нескольких переменных.Так как δz произвольна, непрерывна и обращается в нуль на Γ, то соотношение (3) возможно тогда и только тогда, когда выражение в скобках в (3) равно нулю, т.е. выполнено уравнение Эйлера-Остроградского (2).