Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

ошибки 1 и 2 рода

Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов. Опр. Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н₀ отклоняется, когда Н₀ – верна. Вероятность P{ZÎV_kïH₀}=a.. Опр Ошибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н₀, но в действительности верна альтернативная гипотеза Н₁. Вероятность ошибки второго рода при условии, что гипотеза Н₁ – простая, P{ZÎV\V_kïH₁}=b. Проверка статистических гипотез и доверительных интервалов.Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н₀ – принимается, если значение q₀ накрывается доверительным интервалом, иначе отклоняется.

55. Критерий 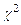и его применение.

Критерий 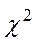применяется в частности для проверки гипотез о виде распределения генеральной совокупности.

Процедура применения критерия для проверки гипотезы H₀, утверждающей, что СВ Х имеет закон распределения 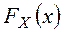состоит из следующих этапов.

Этапы:

1. По выборке найти оценки неизвестных параметров предполагаемого закона .

2. Если Х–СВДТ – определить частоты 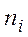, i = 1, 2, …, r, с которым каждое значение встречается в выборке.

Если Х–СВНТ – разбить множество значений на r – непересекающихся интервалов 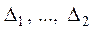и попавших в каждый из этих интервалов .

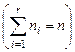3. Х–СВДТ вычислить .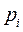

Х–СВНТ вычислить .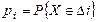

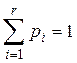
4. .

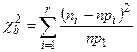5. Принять статистическое решение.

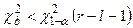– гипотеза Н₀ – принимается.

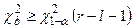– гипотеза Н₀ – отклоняется.

e – количество оцениваемых параметров.

Малочисленные частоты надо будет объединять.

Проверка гипотезы о равномерном распределении генеральной совокупности.

n = 200

А;

№	(xi -1, xi)	ni
	2 – 4		a =0,05
	4 – 6
	6 – 8
	8 – 10
	10 – 12
	12 – 14
	14 – 16
	16 – 18
	18 – 20
	20 – 22

1.

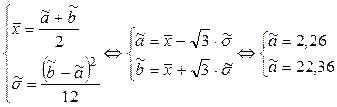
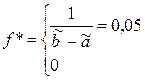
2.

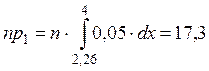
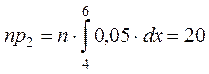
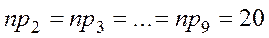
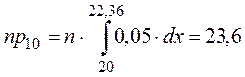
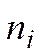
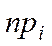
	17,3	0,79
		0,8

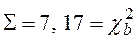
k = 10 – 2 – 1 = 7

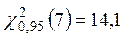
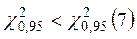– нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.