Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Точечные оценки параметров распределения.

Читайте также:
  1. D-эффект как результат настройки параметров градиентной сетки при ее создании
  2. Анализ имущественного положения организации: цели, источники информации, методы и приемы, показатели оценки структуры баланса.
  3. Анализ традиционной математической модели оценки надежности элемента системы
  4. В ситуации, когда оба участника получили по два флажка на оценку, рефери должен присудить оценки обоим спортсменам.
  5. Взаимодействие и противоречие критериев оценки налоговой системы.
  6. Виды оценки основных средств. Способы начисления амортизации. Учет поступления и выбытия основных средств.
  7. ВОПРОСНИК ДЛЯ ОЦЕНКИ ТЕНДЕНЦИИ ЭВОЛЮЦИИ РЫНКА
  8. ВСЕХ ПАРАМЕТРОВ И ЛУЧШИМИ И ХУДШИМИ НАБОРАМИ ПАРАМЕТРОВ ДЛЯ ПРЕДЫДУЩИХ ПЕРИОДОВ
  9. Вы осознаете и преодолеваете отрицание и оправдания, препятствующие проведению нравственной самооценки.
  10. Вы осознаете необходимость осуществления личной оценки своих как сильных сторон, так и слабостей (дефектов характера).

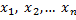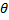Опр. Правило (функция) с помощью которого по выборке находится приближенное значение параметра называется точечной оценкой этого параметра.

Замечания:

1. При априорном рассмотрении – случайной величины также является случайной величиной.

2. Оценку считают «хорошей», если она обладает свойствами:

(a) Несмещенность

(b) Состоятельность

(c) (желательно) эффективность

Опр. Оценка параметра 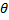называется несмещенной, если . Если , то называется асимптотически несмещенной

Замечание: Несмещенность означает точность оценки «в среднем» отсутствие систематической ошибки.

Опр. Оценка параметра 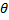называется состоятельной ес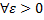ли или 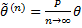. Состоятельность означает возможность за счет увеличения выборки получить любую требуемую точность.

Опр. Несмещенная оценка параметра 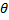называется эффективной если её дисперсия минимальна по сравнению со всеми возможными несмещенными оценками параметра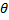

 



Дата добавления: 2015-09-10; просмотров: 76 | Поможем написать вашу работу | Нарушение авторских прав
Случайные события. | Другие свойства | Дисперсия | Следствия из центральной предельной теоремы. | Метод моментов. | Интервальные оценки. Доверительный интервал. Доверительная вероятность. | Доверительный интервал для оценки МО при известной дисперсии | Проверка статистических гипотез | ошибки 1 и 2 рода |

lektsii.net - Лекции.Нет - 2014-2025 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав